централен ъгъл

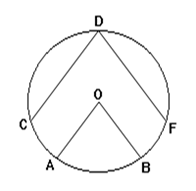
Централен ъгъл - ъгълът, образуван от два радиуса на кръга. Пример централен ъгъл - ъгълът АОВ, ВОС, CDE и така нататък.

На централния ъгъл и дъгата. сключен между страните, каза, че те съвпадат един с друг.

В кръг или в равни кръгове:

1. ако централните ъгли са равни, и съответната дъга равни.

2. ако централните ъгли не са равни, толкова повече от тях съответства до голяма дъга.

Нека AOB и COD са две централен ъгъл, равен или неравно. Сектор АОВ върти около центъра в посоката, указана със стрелка, така че ОА на радиус е подравнен с OC.Togda ако централните ъгли са равни, ОА радиус съвпада с OD, и дъгата AB с диска на дъга.

Така че тези дъги ще бъдат равни.

Ако централните ъгли не са равни, а след това OB на радиус няма да OD, а на някаква друга посока, например, OE или НА. Във всеки случай, по-голям ъгъл, очевидно, съответства на голяма дъга.

Теоремата ни оказа за една обиколка, той остава верен на равни кръгове. защото такива кръгове един не се различава една от друга, с изключение на позицията си.

Обратното също е вярно. В кръг или в равни кръгове:

1. Ако дъгата са равни, и съответните централни ъгли са равни.

2. Ако дъгата не е равно, по-голямата от които съответства на по-голям централен ъгъл.

В кръг или в равни кръгове централен ъгъл са, както съответната дъга. Или ако перифразираме ние откриваме, че централния ъгъл е пропорционална на съответната дъга към него.