Централна симетрия, триъгълници

Централна симетрия - симетрия по отношение на тази точка.

Нека там да се дава една точка О. За да се построи точка симетричен по отношение на точката O точка А, че е необходимо да:

1) Извършва лъч AO.

2) От друга страна на точка O върху отсечка AO Defer OA1 на равен на сегмента AO.

Получената точка А1 симетрична точка А по отношение на точка О.

О точка нарича център на симетрия.

По този начин, точка А и точка относителна A1simmetrichny О, ако О - АА1 средния сегмент. Точка О, се счита за симетричен към себе си.

фигури преобразуване F F1 на фигурата, в която всяка буква А на фигурата F преминава А1 точка симетричен по отношение на дадена точка О, наречен трансформация точка симетрия по отношение на О. Фигури F и F1 се наричат ​​форми, симетрично около точката О.

За да се конструира триъгълник симетрично на триъгълник ABC спрямо точка О, достатъчно е да се конструира точка А1, В1 и С1, симетрични точки А, В и С по отношение на точка О, и да ги свърже с сегменти.

Триъгълници ABC и A1B1C1 са симетрични по отношение на точка О.

Ако симетрия трансформация по отношение на точка O на фигурата се превежда, тогава такава фигура, наречена централно симетрично, и О се нарича център точка на симетрия на фигурата.

Примери за централно симетрични фигури:

Център на симетрия на успоредник - точката на пресичане на диагоналите.

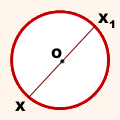
окръжност с център на симетрия - нейния център.

Център на симетрия е права линия, всяка точка на тази линия (т.е. линия има безкраен брой центрове на симетрия).

Трансформация точка симетрия по отношение на движението.