Геометрия на гимназията
В тази глава, ние показваме как да се изгради един равностранен триъгълник. Какво означава "равностранен"? Това просто означава, че и трите страни на триъгълника са с еднаква дължина.
Всеки триъгълник, чиито върхове са точки А. В и С, се записва като △ А Б С
И ако това е равностранен, изглежда, както е показано по-долу:
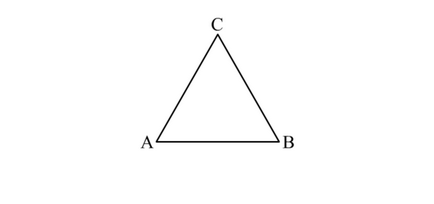
- С помощта на линийка, начертайте линия с произволна дължина. Това ще бъде една от страните на триъгълника.
Ние трябва да се обадите на някой от краищата на сегмента - Един различен - Б.
Сега имаме един сегмент, наречен A B ¯ >>.
Той трябва да изглежда подобно на изображението по-долу. - С помощта на компас, начертайте кръг ∘ А. център, който ще бъде най-А. и радиусът е A B ¯ >>.

- Отново с помощта на компас, начертайте кръг ∘ А. център, който ще бъде в точка Б. и радиусът е A B ¯ >>.

- Можете да видите как кръговете се пресичат (припокриване) на две точки.
Точките са маркирани в червено на снимката по-долу.
- Изберете една от тези точки и да го наричаме В.
Избрахме върха, но можете да изберете дъното, ако предпочитате. Ако изберете най-ниската точка на триъгълника ще се появи "с главата надолу", но тя все още ще бъде вярна.
- Начертайте линия между А и В и да получите сегмент А С ¯ >>.

- Начертайте линия между В и С и да получите един сегмент Б В ¯ >>.

- Строителство △ А Б В завършен.