График производно

Ние считаме, че и сравни графиката на функцията и нейната производна (фигура 1)

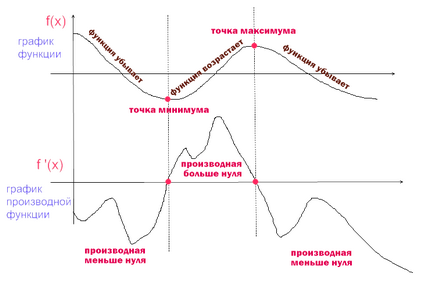
Фигура 1. графика на производното

Графичните имоти производно

1. На интервали, увеличаване производно е положителен. Ако производното в определен момент в някои интервал е положителен, тогава графиката на функцията в този интервал се увеличава.
2. На интервали от намаляване на производно е отрицателен (със знак минус). Ако производното в определен момент в някои интервал е отрицателен, тогава графиката на функцията на интервала намалява.
3. Производното на точка х е равен на наклона на допирателната към графиката на функцията в тази точка.
4. В точките на максимална минимум на производната е нула. Допирателната към графиката на функцията в този момент е успоредна на говедото на ос.

Графиката (Фигура 2) производно определи в коя точка на интервала [-3; 5] функция е увеличен.

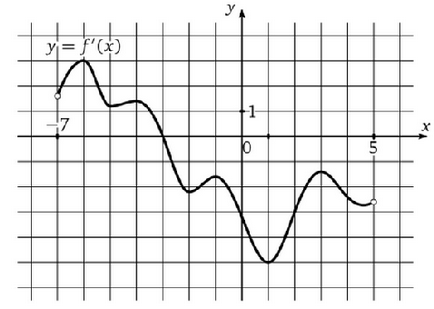
Фигура 2. Графика на производното

Решение: В този момент в производното - е отрицателен, което означава, че функцията намалява от ляво на дясно, и най-високата стойност се намира от лявата страна на -3.

Графиката (Фигура 3), за да се определи количеството на производните максимални точки на интервала [-11; 3].

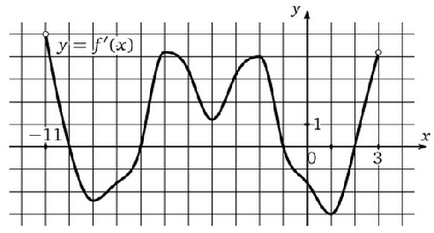
Фигура 3. Графика производно

Решение: максимален брой точки съответстват на точките на знак промяна на деривата от положителна на отрицателна. В тази празнина два пъти функционира промени знак плюс минус - при -10 и -1 точка. Следователно максималният брой точки - две.

Графиката (Фигура 3), за да се определи количеството на производното на минимални точки на интервала [-11; -1].

Решение: Минималните точки съответстват на точките на знак промяна на деривата от отрицателни към положителни. В този момент в този момент тя е само -7. Следователно, минималния брой точки на предварително определен интервал - един.

Графиката (Фигура 3), за да се определи количеството на деривати екстремум точки.

Решение: екстремуми са точки, колкото минималната и максималната. Намерете броя на точките, в които се регистрират на деривативни промени:

• Точка 10 (макс)
• Точка -7 (минимум)
• Точка -1 (макс)
• Точка 2 (мин)

Функция съдържа 4 екстремни.