Изграждане на права крива - елипса, парабола и хипербола, рисуване за ученици

Отделни части на овала са криви на постоянна кривина могат да се направят с дебеломер и следователно те се наричат ​​кръгови криви. Криви с променлива кривина се изтегля през криви и права, посочени криви. За линейни криви включват елипса, парабола, хипербола, кръг еволвентен, циклоидални различни видове, синусоида, различни спирали. Много прави-криви са оформени от плоските части на различни повърхности. Така, например, елипса, парабола и хипербола са образувани при пресичането на повърхностни равнини на различен ъгъл конус.

Ellipse. Мястото на точки в равнината, сумата от разстоянията, от които до две дадени точки, наречени фокуси, е постоянна, се нарича елипса. Има много начини за изготвяне елипса. Най-често е метод на две среди, диаметрите на които са равни на Основните и второстепенни оси на елипсата. Ако през центъра О прекарват произволен диаметър, след това пресича окръжността в точки Е, F и G, Н. Чрез тези точки се извършва, линии, успоредни на осите на елипсата; пресечната точка на тези две линии се определят елипса точка К и L. Обикновено диаметърът на проводника, един от разделителните обиколката на 12 равни части.

Да предположим, че искате да се поберат елипса на успоредник. Вземете долната страна на успоредник страна на площада, построен на площада, и тя се вписва в неговия кръг. Окръжност център О ще съответства на центъра О 'на елипсата, на диаметъра на кръга AB ще съответства диаметър конюгат "В" на елипсата, и така нататък. D. Разделете половината OD диаметър и половината от диаметъра на конюгиран Ò'Ð "в равни части (например четири) и се провежда чрез линии, разделящи точка успоредна на AB. На съответните линии ще бъде съответните точки на кръг и елипса, например Е и Е '. Получава се през тези точки на многоъгълни прави успоредни наклонени ODO ". В технология, многоточието се намират в спиците на маховика, в елиптични предавки.

Фиг. 1. Изграждане на елипсоид. Строителство на елипсата вписан в успоредник

Парабола. Мястото на точки в равнината на еднакво разстояние от дадена точка, която е в центъра, а на дадена линия, направляващата на който се нарича парабола. Най-често е необходимо да се конструира парабола, съвпадение преките различни посоки (фиг. 2а). За да се конструира парабола в раздел AB разделят линия сегменти АВ и OB в същия брой равни части, означават разделяне точки в последователност, 1-5, 1-5; определени точки еднакво се свързват и да носят направо тангента крива към семейството на прави линии.

Фиг. 2. Изграждане на парабола

Може да се изгради парабола от своя връх А и произволна точка В (фиг. 2Ь). Към това се извършва през точката A AC парабола ос; изгради върху него ADBC ​​правоъгълник; разделят страни на правоъгълника и означават същите, както в предишния случай; чрез разделителни точки на линия АД се извършва сегменти успоредна на оста на парабола, и разделяне на точки на правата линия DB, свързан с върха на парабола А; точката на пресичане на линиите, минаващи през точките означени със същите обозначителни номера ще бъде парабола точки (точки I, II, III).

Хипербола. Мястото на точки в равнината, разликата в разстоянията което двете предварително определени места (огнища) е с постоянна стойност, наречена хипербола. Хипербола в техническо чертане е намерена в някои части на конична форма, се скъсява, като самолети. Кривата обикновено изработена с използване на методи на описателен геометрия. Геометрични методи за конструиране на тази крива не се характеризира с простота; Тук е един от тях. За да се конструира от двете страни на ъгъла на хипербола AO и OB (асимптоти) и точка В се извършва чрез тази точка на линия, паралелна на асимптоти (фиг. 3). След това се прекрачва границата греди O1. O2 и т. D. и пресечните точки на лъчите отново извършват паралелни линии асимптоти взаимното им преминаване в точки 11 и 21. Тези точки са точки на хипербола. хипербола клон, като същевременно продължава да сезира асимптоти, но почти никога не се срещне с тях. Има и друг практически метод за изграждане хипербола.

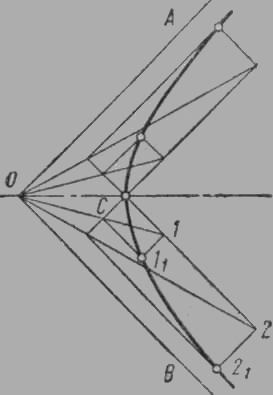
Фиг. 3. Изграждане на хипербола

На нашия сайт можете да намерите необходимата подробна и точна информация за колата Lada Priora - снимки, описания, спецификации, оборудване вътрешното производство колата, и можете да намерите и прегледи на автомобили Лада.