Как да намерите областта на кръг

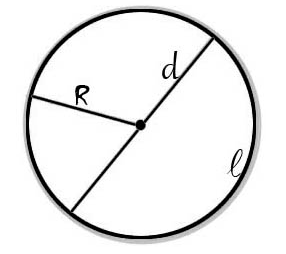
Голям брой точки, разположени на еднакво разстояние от центъра и се намира на същото разстояние - obrazuyutkrug. равнина фигура. Радиусът на кръга - линия, която свързва центъра на кръга до всяка точка на нейната обиколка. В същото време в един и същи кръг, което не би искала да посочи диапазон ще бъде същото. диаметър Circle - сегмент, излъчвана от всяка точка на окръжността, минаваща през средата на кръга и завършва паралелно в същата обиколка.

Как да намерите областта на кръг. площ на кръг се изчислява чрез формулата: където състоеше числата.

Интересен факт. Номер. Той представлява съотношението между дължината и обиколката на същия диаметър кръг. Когато това е с постоянна стойност. И как можем да знаем? = 3.1415926 и се прилага от 1737.

Същият областта на кръг с диаметър е дадено от

S = (? / 4) г 2

Нека разгледаме, за по-голяма яснота,
Ние намираме областта на кръг с помощта на диагоналите му. Вземете радиус от 4 см.

решение
1) изчисли с диаметър, който е по-голям от два пъти радиуса.
г = 2R
г = 2 * 4 = 8
2) Заместването стойности във формулата
S = (3,14 / 4) * 2 Август = 0.785 * 64 = 50,24
Ако проверявате отговора, даден на предишното, те са равни.

Когато ние търсим област или сегмент от сектора кръг, е много полезно знание на основните формули. С тяхна помощ, те не могат да признаят като се знаят.
Сегмент - се нарича ограничена част от кръга, която е ограничена от акорда и дъгата на окръжността.
Както вече знаете, района на изчисление на кръг се изчислява въз основа на броя. пъти радиуса на квадрат. Използването на дължината на окръжността, можем да намерим радиуса.

Ако заместим тази формула във формулата за изчисляване на района. ние ще получи:

Нека разгледаме, за по-голяма яснота,
Намери площ на кръг с обиколка, равна на 8 см.
решение
Ние използваме формула S = 8 2/4 * 3.14 = 64 / 12.56 = 5 cm