Как да намерите тангента, ако е известен косинус

Концепцията на допирателната е основен в тригонометрията. Тя се отнася до някои тригонометрични функция, която е периодична, но не непрекъснато в областта като задължително и косинус. И има прекъсвания в точките (+, -) * п + Pi Pi / 2, където п - е периодът на функцията. В България тя е обозначена като TG (х). Тя може да бъде представляван от всички тригонометрични функции, като всички те са тясно свързани помежду си.

ще трябва

• Учебникът по тригонометрия.

инструкция

За да се експресира допирателната на ъгъл чрез синус, е необходимо да се припомни геометричната определението на допирателната. Така че, допирателната на остър ъгъл в правоъгълен триъгълник, е отношението на другия крак в съседна.

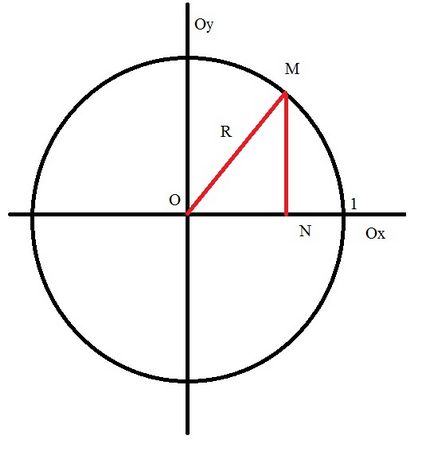
От друга страна, разгледа Декартова координатна система, в която единица кръг е изобразена с радиус R = 1 и център О в основата. Обърнете обратно на часовниковата стрелка въртене, както положителни, и отрицателни в обратната посока.

Имайте предвид, определен момент M на кръга. От това по-ниско, перпендикулярно на оста Ox, обадете си точка Н. триъгълник резултат OMN, което ONM ъгъл е прав.

А сега да разгледаме малък ъгъл MON по дефиниция синуса и косинус на острия ъгъл и в правоъгълен триъгълник
грях (пн) = MN / ОМ, COS (MON) = ON / ОМ. Тогава MN = грях (MON) * OM, а на = косинус (MON) * ОМ.

Връщайки се към геометричната определението на допирателната (Tg (MON) = MN / ON), заменен експресията, получен по-горе. След това:
TG (MON) = грях (пн) * ОМ / COS (MON) * ОМ, намали OM, след TG (MON) = грях (MON) / COS (MON).

косинус "клас =" lightbx "данни Лайтбокс =" статия образ ">

От основните тригонометрични идентичности (грях ^ 2 (X) + защото ^ 2 (х) = 1) експресира косинус. чрез задължително: COS (X) = (1-грях ^ 2 (х)) ^ 0,5 заместител тази експресия в получена в етап 5. След TG (MON) = грях (пн) / (1-грях ^ 2 (MON )) = 0.5.

Понякога е необходимо при изчисляването на допирателната на двойни и половин ъгъл. Тук също отношения са получени: TG (х / 2) = (1-COS (х)) / грях (х) = (1- (1-грях ^ 2 (х)) ^ 0,5) / грях (х) - TG (2х) = 2 * TG (х) / (1-TG ^ 2 (х)) = 2 * грях (х) / (1-грях ^ 2 (х)) ^ 0,5 / (1-грях ( х) / (1-грях ^ 2 (х)) ^ 0,5) ^ 2) =
= 2 * грях (х) / (1-грях ^ 2 (х)) ^ 0,5 / (1-грях ^ 2 (х) / (1-грях ^ 2 (х)).

Възможно е също така да се изрази квадрата на допирателната през ъгъл косинус и или синус двойно. TG ^ 2 (х) = (1-COS (2х)) / (1 + COS (2х)) = (1-1 + 2 * грях ^ 2 (х)) / (1 + 1-2 * грях ^ 2 (х)) = (син ^ 2 (х)) / (1-грях ^ 2 (х)).

Обърнете внимание на допустимите граници при решаване на уравнения и неравенства.

Познаването на основния идентичности сърце, бързо ще скочи от единия към другия тригонометричните функции.