Как да решим квадратни неравенства
В предишния урок обсъждахме как да се реши линейни неравенства. Но за разлика от квадрата на линейни неравенства се решават много по-различен начин.
по същия начин, като линеен квадратното неравенство не може да бъде решен!
За решаването на квадратни неравенства използва специален метод, който се нарича интервали метод.
Какво е метод интервал
метод интервали нарича специален начин за решаване на квадратни неравенства. По-долу ще обясним как да се използва този метод и защо той получава своето име.
За решаването на квадратното неравенство метод на интервали, необходими:
- преместите всички членове на неравенството към лявата страна, така че само нула е в правото;
- уверете се, че неизвестен «х 2" е положителен фактор;
- равнява на лявата страна на неравенството на нула и решаване на получената квадратно уравнение;
- получен корените на място на брой линия във възходящ ред;
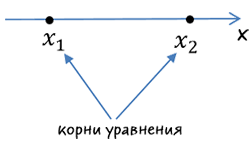
- нарисува "дъга" на интервалите. От дясно на ляво, като се започне с "+" остави променлив знаци "+" и "-";
- изберете необходимите интервали и да ги запишете в замяна.
Ние разбираме, че правилата, описани по-горе, е трудно да се възприемат само на теория, така че да вземем за пример за решаване на квадратното неравенство в алгоритъма по-горе.
Необходими за решаване на квадратното неравенство.
х 2 + х - Декември 2 + х - 12 Февруари "е положителен коефициент. В неравенството "х 2 + х - 12 февруари" е на стойност положителен коефициент "1", а след това отново, ние не се нуждаят от нищо.
Съгласно претенция 3 се равнява на лявата страна на неравенството на нула и решаване на квадратно уравнение получен.
х 2 + х - 12 = 0
1 ± √ 1 с 2 - 4 · 1 · (-12)
Сега, съгласно претенция 4, ние отбелязваме, получена при корените на недвижими ред във възходящ ред.
Не забравяйте, че, въз основа на какви неравенство пред нас (строга или не строг) отбелязваме точка на реалната ос по различни начини.
Сега, както е посочено в претенция 5. нарисува "арка" през интервалите между отбелязаните точки.
Залепете знаци в интервали от време. Променлив от дясно на ляво, като се започне с "+" марка с.
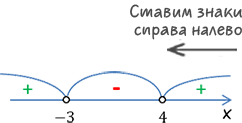
Ние просто трябва да се приложи параграф 6, което е, да изберете желаните интервали и да ги запишете в замяна. Обратно към нашия неравенство.
Тъй като това неравенство «х 2 + х - 12 2 + х - 12 2 + х - 12 + 2 0 - 12 2 + х - 12 2 + х - 12 2 + х - 12 = 0
1 ± √ 1 с 2 - 4 · 1 · (-12)
При определяне на какви интервали трябва да се предприемат в отговор, е необходимо да се придвижат от най-скорошните промени в неравенството, преди да намери корените си.
В нашия случай, най-новата версия на неравенството преди да търсите корените на тази «х 2 + 3x - 4 ≤ 0".
Така че интервалите трябва да бъдат избрани да се отговори със знак "-".
0 "/> Отговор: -1 ≤ х ≤ 4
За съжаление, решаване на квадратното неравенство не винаги да се окаже, двете корените и всичко върви според общия устройствен план по-горе. Може да има случаи, когато се оказва един корен, или дори един-единствен корен.
Как да решим квадратното неравенство в такива случаи, ние ще обсъдим в следващия урок, "корен квадратен от неравенството на с един или без корени."