Както превежда десетична дроб в обикновен метод 3
Тук, изглежда, десетичната в обичайните - начално тема, но много студенти не го разбират! Така че днес, ние ще обсъдим няколко алгоритми, с които ще се разбират с всички фракции, само за секунда.
Позволете ми да ви напомня, че има най-малко две форми на записване на една и съща снимка: обикновени и десетични. Цифри след десетичния знак - това е всички видове дизайн тип 0,75; 1,33; и дори -7.41. Но примери на фракции, които експресират същите номера:
Сега ние трябва да се разбере как знака след десетичната вписвания отиват в обичайните? И най-важното, как да го направя възможно най-бързо?
Основният алгоритъм
В действителност, има най-малко два алгоритъма. И сега ние ще разгледаме и двете. Нека започнем с първата - най-прост и разбираем.
За да се превърне десетична към вулгарни, трябва да извършите три стъпки:
- Препишете оригиналната снимка като нова фракция: числителят ще остане на първоначалното десетичната а знаменателят е необходимо да поставите модула. Знакът на самото число се поставя в числителя. Например:
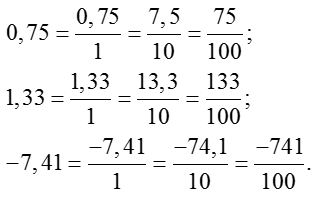
Важна забележка за отрицателните числа. Ако оригиналният примера на десетичната част е знак "минус", а след това подаде към общата фракция също трябва да е "негативна". Ето няколко примера:
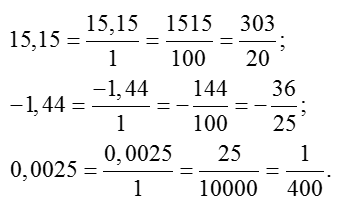
Особено внимание следва да се обърне на последния пример. Както виждаме, има много малка част от 0.0025 нули след десетичната запетая. Поради тази причина ние имаме вече толкова, колкото четири пъти, за да умножим числителя и знаменателя на 10. Мога ли по някакъв начин да опрости алгоритъм в този случай?
Разбира се, че можеш. И сега погледнем към алтернативен алгоритъм - тя е малко по-трудно да се разбере, но след малко практика работи много по-бързо от стандартните.
По-бърз начин
Алгоритъмът също 3 стъпки. За да получите една малка част от обичайната десетичната, направете следното:
- Изчислете колко цифри след десетичната запетая е на стойност. Например, част 1.75 от две числа, и при 0.0025 - четири. Ще означаваме този номер с писмо $ N $ на.
- Препишете първоначалния брой като част от формуляра $ \ Frac ^ >> $, където $ на $ - това е всички цифри на първоначалната фракция (без "Старт" отляво нули, ако има такива) и $ N $ - това е броя на цифрите след десетичната запетая, ние се счита първата стъпка. С други думи, необходимо е да се разделят на първоначалните цифри от фракцията на единица до $ п $ нули.
- Ако е възможно, да се намали получената фракция.
Това е! На пръв поглед, тази верига е по-трудно предишния. Но в действителност, той и по-лесно и по-бързо. Преценете сами:
Както можете да видите, в частта от 0,64 след точката е на стойност две числа - 6 и 4. Поради това, $ п = 2 $. Ако премахнете запетаята и нули от лявата страна (в този случай - само една нула), получаваме числото 64. Отидете на втората стъпка: $> => = $ 100, така че в знаменателя е точно сто. Е, тогава може да се намали само на числителя и знаменателя. :)
Друг пример:
Тук всичко е малко по-сложно. На първо място, номера след точката на десетичната има 3 броя, т.е. $ п = 3 $, така че ще трябва да участва в $ ^> ^> = $ 1,000. На второ място, ако премахнете от десетичната запетая, стигнахме до тук е: 0004 → 0004. Спомнете си, че нулите в ляво трябва да бъдат премахнати, така че в действителност имаме броя 4. След това, всичко е проста: разделяй, нарязани и да получите отговор.
Накрая, последният пример:
Особеността на тази фракция - наличието на цялата страна. Ето защо, на изхода получаваме неадекватно фракция 47/25. Вие със сигурност може да се опита да се раздели 47 до 25 с остатък и по този начин да преразпределят част от цялото. Но защо да усложни живота си, ако тя може да бъде направено в етап на трансформация? Е, изправени пред него.
Какво да правим с цялата страна
Всъщност, всичко е много просто: ако искаме да получите право изстрел, е необходимо да се отстрани от него през цялото време от страна на промените, и след това, когато стигнем резултата, отново, за да го добавите точно преди наклонената черта.
Да вземем например един и същ номер: 1.88. Zabem единица (число част) и поглед към част от 0.88. Тя може лесно да се трансформира:
После си спомни за "загубени" един от предната и добавя:
Това е! Отговорът се оказа същият като този, след отделянето на целия последен път. А още няколко примера:
Това е красотата на математиката: какъвто начин и да отидеш, ако всички изчисления са верни, отговорът винаги ще бъде една и съща :).
В заключение бих искал да помисли за друг метод, който помага много.
Трансформации "на слух"
Нека да помислим за това, всичко е десетична. По-точно, тъй като ние я прочете. Например, броят 0.64 - ние го прочете като "нула цяло, 64 стотни", нали? Е, или просто "64 цента". Ключовата дума тук - "цента", т.е. номер 100.
Какво ще кажете за 0004? Тази същата "нула цяло и 4000на" или просто "четири хилядни." Както и да е, ключовата дума - "хилядни", т.е. 1000.
И така, какво толкова има? А фактът, че тези номера в крайна сметка "флоат" в знаменателя на втората фаза на алгоритъма. Т.е. 0.004 - на "четири хилядни" или "4 разделена на 1000":
Опитайте се да работят за себе си - това е много проста. Основното нещо - да се чете правилно оригиналната снимка. Например, 2,5 - за "две цели, пет десети", така че
А някои 1125 - са "едно цяло, 125,000th", така че
В последния пример, разбира се, някой ще възрази, като каза, че не всеки студент Очевидно е, че 1000 се дели на 125. Но трябва да се помни, че 1000 = 10 = 3 и 10 2 ∙ 5, така че
\ [\ Започнете 1000 = 10 \ cdot 10 \ cdot 10 = 2 \ cdot 5 \ cdot 2 \ cdot 5 \ cdot 2 \ cdot 5 = \\ = 2 \ cdot 2 \ cdot 2 \ cdot 5 \ cdot 5 \ cdot 5 = 8 \ cdot 125 \ край \]
По този начин, всяка степен на десетки разширява само по коефициент 2 и 5 - това са факторите, които трябва да се търси в числителя, така че в крайна сметка всичко падна.
В този урок е приключила. Ние се обръщаме към по-сложна операция обратна връзка - виж "Преходът от необичайно в десетична дроб.".
- сравняване на фракции
- Повтаряйки десетични
- Как да се изчисли по-бързо логаритми
- Събиране и изваждане на десетични дроби
- Опростява задачата на решението за промяна на променливата
- Задача B4: Семейство от трима души, водещи от Москва до Нижни Новгород
- Безплатна Подготовка за изпита 7 прости, но много полезни уроци + домашна работа
