Какво е стационарни и критични точки за това как да ги намерите

На първо място, ние напише уравнението на математическа функция

където х - функция аргумент, и по-- самата функция. Това означава, че ние се всяка стойност на аргумент х, и се изчислява по уравнението (1) стойността на функцията в тази точка. Приемат се изготвя графиката на у = е (х). Съставяне на оси х и у координати. X стойност нанесена по протежение на хоризонталната ос х. Тази ос се нарича оста х. Вертикална отложи изчислената стойност на функция у (тази ос се нарича вертикална ос). Фигурата е графика на функция

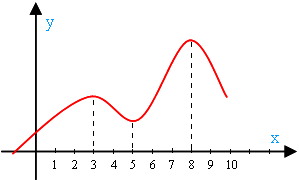
Както можем да видим при х = 3 и х = 8 функция на максимум. И когато х = 5, функцията има минимум. Това означава, че функция у = F (X) може да има минимум, така и максимуми. така

Максималната точка - стойността на х за които функцията има максимален.

минимална точка - стойността на х за които функцията има минимум.

И на тези точки се нарича общата дума - крайност. Това означава, че в точките на екстремум функция има максимална или минимална стойност.

Ние все още трябва да знаем какво е производната на функцията. Ако знаем, самата (1) функция, а след това на деривата се приема, както следва:

Значението на производно - наклона на функцията на точка х. Тя може да се проведе при всяка точка на функцията на допирателната линия и ъгълът между тази тангента и оста х определя ъгъла на наклон. Но това е по-удобно да се изчисли не ъгъла а наклон, и допирателната на Тд на ъгъл. С други думи,

tgα = Dy / DX = DF (х) / DX (3)

Както се вижда от фигурата горе в точки екстремум функция tgα = 0. Това означава, че производното на тези точки е равна на нула. Ако знаем, функцията на уравнение (1), за създаване на производна на нула, ние получаваме алгебрични уравнение за изчисляване на максимални и минимални точки

И това, което е критично и стационарни точки на функцията? функция Extremum точка (тоест, когато функцията е с максимална или минимална), понякога наричан също фиксирани точки. Това е фигурата над точката х = 3, 5 и 8. Това понякога се случва, че у функция (х) има краища, т.е. функцията крива не излиза до безкрайност или наляво или надясно. Например, на горната фигура, ще се приеме, че тази функция се намира между точките х = 1 и х = 10. Ако в крайните точки на тези функция ще имат минимална (или максимум), т.е. екстремум (производното е нула), тогава тези точки не нарича неподвижна.

Но вътрешните точки на функцията при които функцията е непрекъсната, но в тези точки производна не съществува, наречени критични точки. Виж фигурата по-долу

В точката х = 0, тази функция има максимална, но в този момент има фрактура и функции. Остър връх. Производното (наклона на функцията) вляво от точката х = 0 е положителна, и отдясно на тази точка производното е отрицателен. Това е критичен момент. Но в точката х = 1 има минимален (производното е нула), но функцията променя знак без счупване (т.е. постепенно). Това е минималната точка и фиксирана точка.