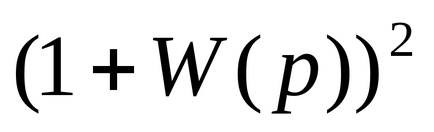Linear интегрирана оценка
Най-добре е линейна интегрална оценка неразделна оценка
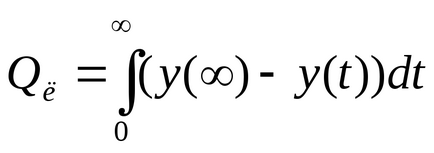
която е равна на площта между линията на затворници
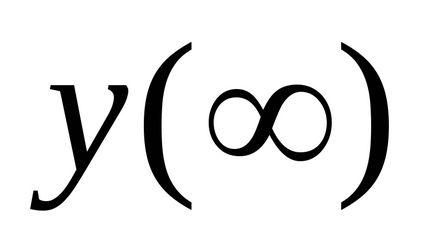
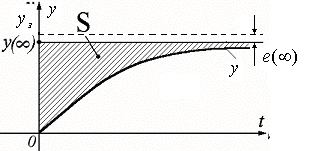
Интегрална оценка се вземат предвид както степента на динамични вариации, както и продължителността на тяхното съществуване. Следователно, долната оценка (площ S), по-добре процесите за контрол на качеството, толкова по-бързо краищата PP, по-малките отклонението на сигнала у (т) от Й.З..
Разликата под неразделна знак или преходът е динамичният компонент на сигнал за грешка:
.
Ето защо, линейна интегрална оценка често се определя в следния вид:
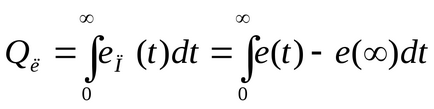
метод Kulebakin
.
Помислете за следната функция трансфер:
.
В етап разглежда въздействието на R (т), като х (т) на входния сигнал.
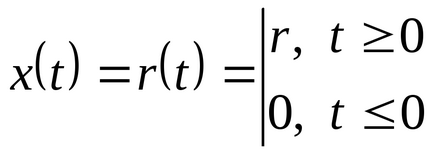
Интегралната схема ще изглежда така:
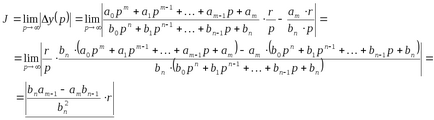
Ако говорим за минимум от тази функция, тя ще бъде постигната при равенство
идеалното преходно (S площ - мин).
по този начин избор на коефициентите на предавателната функция в съответствие с уравнение (*) може да се постигне предварително определени показатели за качество.
Модулната комплексна оценка
Но в ущърб на линейната интегрирана оценка е, че тя може да се използва само за монотонни (непериодични) преходни процеси.
Интегралът се изчислява за кривата на променлив ще бъде значително по-малко от 1. неразделна, изчислена за апериодична крива 2, въпреки че кривата на качество за PP 2 ясно по-добре.
В тази връзка, да се прилагат преходни колебания като неразделна променливо оценка знак подинтегрален които по някакъв начин се елиминира. Тези прогнози са, например, модулната интегрирана клас (MRE - интеграл от модула за грешка):
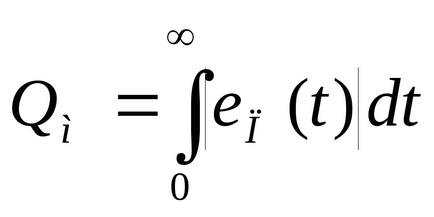
И нейното изменение (IVMO - претеглена неразделна модула за грешка)
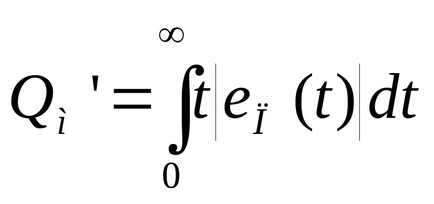
Тази оценка дава повече тежест на сигнала стойностите на грешките, които се срещат в края на платката.
Квадратичен неразделна оценка
За осцилаторна процеси най-често използваните неразделна квадратичен клас (PPI - неразделна квадратична грешка), което се определя от формулата:
,
която е равна на площта под кривата
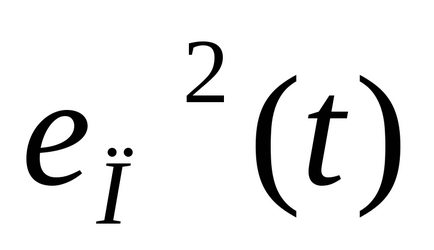
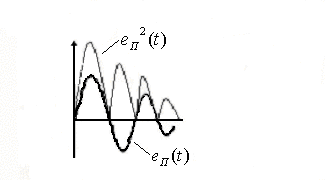
Квадратичен оценка, както и линеен и взема под внимание степента и продължителността на отклоненията. Въпреки това, поради изграждане на сигнала
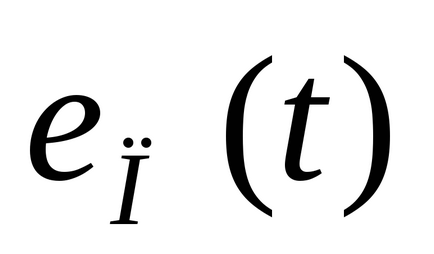
на площада, първите (големи) отклоненията стават окончателната стойност на интегралната значително по-голяма тежест, отколкото следващите (малки) отклонения. Следователно, минималната стойност за оценка винаги съответства на колебания процеси с ниско затихване.
Изчисленията използват също IWCO.
Приложна и подобрена квадратичен оценка, които, с изключение на отклонение, с тегловен коефициент отчита отклонения деривати.
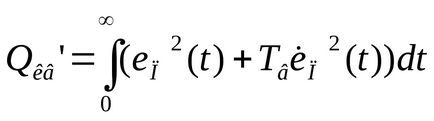
Обикновено, тегловният коефициент е избран равно на желаното време се повиши или да вземе в
Апериодични неразделна оценка
защото всички стойности са константи. Когато Т - времеконстанта, която се дава.
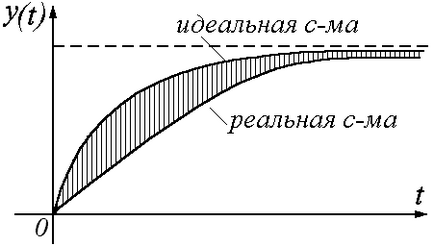
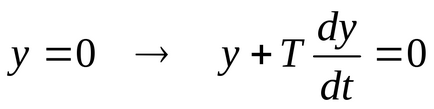
J функцията заема минимална стойност. Това ще бъде постигнато в случая, ако - апериодична преходно.
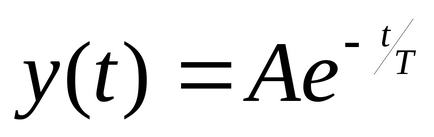
Трябва да се отбележи, че абсолютната стойност на всяко самата интегрална оценка, не е от значение. Те служат само за сравнение на различните варианти за персонализиране на една и съща система.
Функцията за прехвърляне на затворена система е както следва:
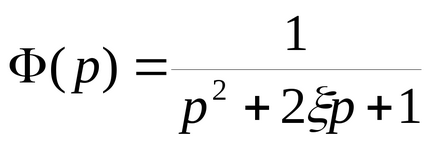
три оценка на качеството обсъдени (с поетапно експозиция).
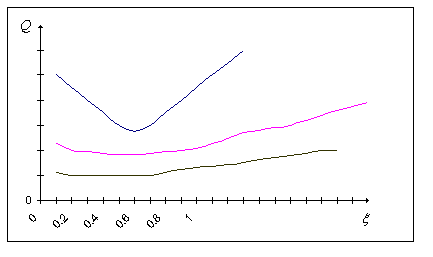
До сега ние приехме, че стойността на параметрите на обекта и управляващия блок продължава да работи на постоянна система. Въпреки това, в реална индустриална среда, поради няколко причини (промяна в температурата, износване, стареене на изолацията) на параметрите на системата се променят постепенно, както и техните реални стойности са винаги различни от изчислението.
Влияние на вариации на системните параметри на статичните и динамични свойства се наричат параметрични сътресения. и където получените характеристики на отклонението система от изчислените стойности -parameter грешки (грешки).
Чувствителност на системата се нарича промяна на изходните характеристики или качество в зависимост от промените в параметрите на системата. Ако системата не се променя неговите изходни характеристики или качествени показатели при смяна на параметрите на системата, такава система се нарича груби (стабилна).
Количествена характеристика на чувствителността на системата е функция на чувствителност. която се определя като частично производно на характеристика система (прехвърлянето, преходни времето за реагиране и преходно т.н.) на променливи параметри, например
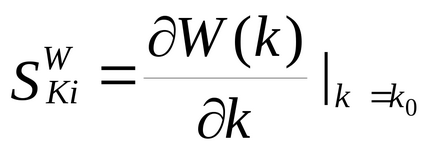
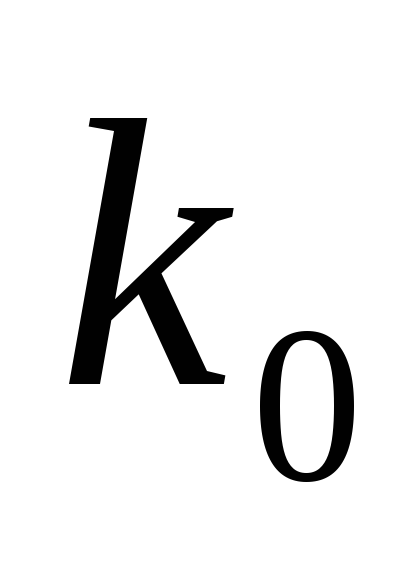
Най-често се използва в практиката функция относителна чувствителност:
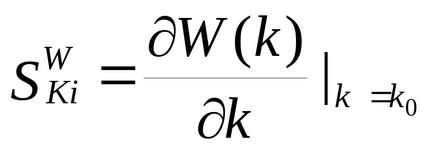
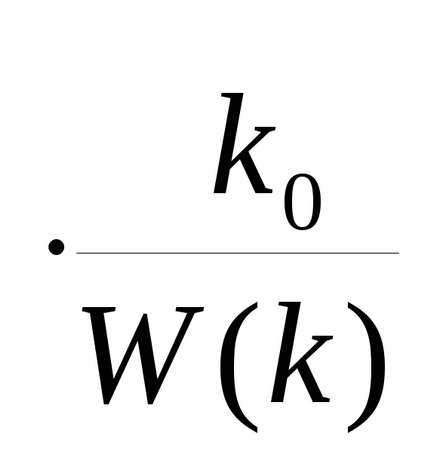
По-малкият функция чувствителността (относителна функция чувствителност), системата и по този начин по-добър контрол на качеството грубата.
В системни параметри промяна отворен цикъл води до изходната стойност отклонение от желаната стойност. Затворена система, а напротив, се чувства това отклонение и се опитва да я поправи. Ето защо, чувствителността на системата към промени в параметрите - това е въпрос от първостепенно значение. Основното предимство на системи с операционната система - в способността си да се намали чувствителността към промени в параметрите.
Да разгледаме случая, когато обектът чрез промяна на параметрите на своята предавателна функция на приетото израз
Ако системата е отворена, променливата за производствената (като Лаплас изображение) се увеличава:
В затворена система:
Ако приемем, че
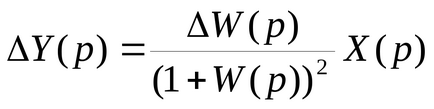
Този израз показва, че в изходния затворена система променлива промяна е намалена