Линиите и самолети - studopediya

Фиг. Фигура 4.17. 4.18

Ако равнината, определена пресичащи се прави линии (фиг. 4.17), след това разтворът е да се извърши през точката Двойка прави линии успоредно зададени.

Ако равнината, определена писти (4.18), след изграждането може да се извърши по следния алгоритъм:

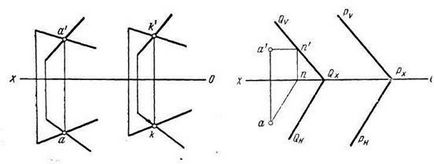
1. След провеждане на точка А, например, желаната хоризонтална равнина Q, паралелни контури предварително равнина P.

2. Чрез тази хоризонтална равнина, успоредна изпълнява даден желания. Предна следа QV изготвят чрез предна проекция р 'предната следа PV хоризонтално паралелно път; хоризонтална следа QH - през точката QX паралелен път RN.

Задача 2. Чрез точка А (а, а ') да държи Р. равнина, перпендикулярна на правата линия (фиг. 4.19).

а) Трябва да покажем най-желаната самолетни пресичащи се линии. В този случай, най-простите за конструиране Q равнинни основни линии - хоризонтална предна и минаваща през точка А (а, а ').

Фиг. Фигура 4.19. 4.20

б) Трябва да покажем на желаните самолетни следи. Конструкцията може да се извършва от следния алгоритъм. Чрез хоризонтална равнина провеждане Q перпендикулярна на отсечката BC. След това чрез хоризонталният задръжте желания равнината, перпендикулярна на правата линия преди новата ера. Предна следа QV изготвят чрез фронтална проекция р 'предната следа в хоризонтално направление перпендикулярно Б "; хоризонтална следа QH чрез точки QX перпендикуляра към Христа.

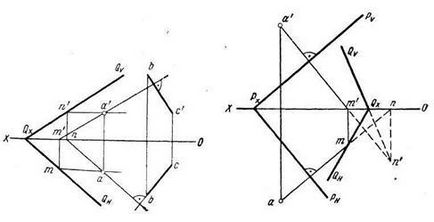
Задача 3. Чрез точка А (а, а ') да държи Q равнина, перпендикулярна на предварително определена равнина Р и преминаваща през точката на изчезване оста следа QX X (фиг. 4.20).

Известно е, че Q равнина е перпендикулярна на предварително определена равнина Р, когато тя преминава през перпендикуляра към него или перпендикулярна линия лежи в равнината P.

Фиг. 4.20 Решението на проблема се извършва по план, а след това първият от тези условия:

1. След предварително определена точка А проведе перпендикулярна на равнината Р (съм # 9524; PH a'm '# 9524 ;. PV).

2. Чрез този перпендикулярна точка и предварително определена QX която остава желаната равнина Р. В този случай, следата Qn проведено чрез хоризонтална проекция на m хоризонтална и перпендикулярна точка следа QX; проследи QV - от предната проекция N 'предната следа и перпендикулярна точка QX.

Желаният самолета може да бъде построен и пресичащи се линии, ако през точката QX проведе преки, които имат обща точка с перпендикуляра.

Задача 4. Чрез точка А (а, а ') нарисувате права линия, перпендикулярна на линия преди новата ера.

Вие перпендикулярно лежи в равнина, перпендикулярна на дадената линия преди новата ера. Ето защо, проблемът може да бъде решен чрез следния алгоритъм:

1. След точка на задържане равнина Р. перпендикулярна на линията BC.

2. Определяне на точка К (к, к ") пресичане с права линия BC Q равнина посредством хоризонтално стърчащата равнина S.

3. Прилагане на точките А и К.

В диаграмата, решаване на проблема на този алгоритъм, е възможно да се покаже равнина две пресичащи основните линии (з х е) (фиг. 4.21) или писти (фиг. 4.22).

Фиг. Фигура 4.21. 4.22

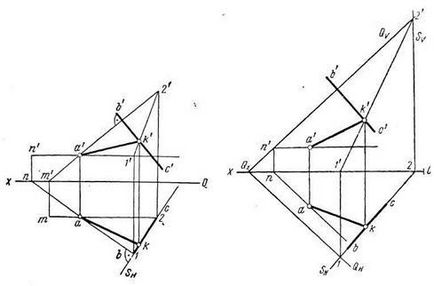
Задача 5. Изграждане на линия на пресичане на самолетите ABC и DEF.

Този проблем може да бъде решен с използването на задачата, в пресечната точка на правата линия и равнина. Фиг. 4.23 илюстрира структурата на линията на пресичане на равнините, определени от триъгълници ABC и DEF. Line MN въз основа на намерени точките на пресичане на страни DF и EF DEF триъгълник с равнината на триъгълника ABC.

Например, за да се намери точката на пресичане на M DF страна с ABC равнина. DF извършва чрез директно предна равнина Р. прогнозира, че пресича равнината на триъгълник ABC в права линия I II. В сечението на хоризонталните проекции на DF и 12 получават хоризонтална проекция m на необходимата точка М. Тогава намери пред проекция m 'N точка М. точка на пресичане с права линия EF ABC равнина намерени предния очаква Р. равнина, която пресича равнината на триъгълник ABC направо III IV. В точката на пресичане на хоризонтален издатини EF и 34 получават хоризонтална проекция п на желаната точка N.

Комбинирането на двойки точка м и п ', m и п. получават пресечната точка на проекционна линия MN ABC и DEF равнини.

Видимост части сегменти равнини, определени по реда на конкурентни точки.