Магически квадрат (магически квадрат)

Добре дошли в света на пъзели, оптични
Илюзии и интелектуално забавление Трябва ли да се доверяват на това, което виждате? Можеш ли да видиш, че никой не е виждал? Вярно ли е, че неподвижни обекти могат да се движат? Защо възрастни и деца виждат една и съща тема по различен начин? На този сайт ще намерите отговори на тези и много други въпроси.

Поздрави! Вие искате да станете един от нас? Определя # 133;






Ако вече сте един от нас, на входа тук.

Американски актьор Джон Ueyn (1907-1979) по някакъв начин печели на карти Ласи куче.

Магически квадрат (магически квадрат)

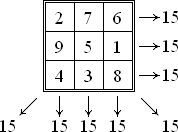
Магически или магически квадрат - квадратна масив N х N, N 2 пълни числа, така че сумата от числата във всеки ред, всяка колона и от двете диагоналите на същите. Ако квадратен сумата от числата са равни само в редове и колони, той се нарича semimagic. Нормални наречени магически квадратни попълнено цели числа от 1 до 2. п магически квадрат се нарича асоциативни или симетрични ако сумата на всеки две числа, разположени симетрично по отношение на центъра на квадрата е равно на 2 п + 1.

квадратен Ло Шу - уникален нормално магически квадрат 3 × 3. Е бил известен в древен Китай, първото изображение върху външната обвивка на костенурка датира от 2200 г. пр.н.е.

Изображение Ло Шу книга Минг

Devil магически квадрат - магически квадрат, което съвпада с магически постоянна сумата от броя на разбито диагонал (диагонал, които са образувани чрез прегъване на квадратен в тора) в двете посоки. Тези квадрати се наричат ​​още pandiagonalnymi. Там дяволските магически квадрати 48 4 × 4 до ротации и разсъждения.

Магически квадрат от 4 × 4, изобразен на гравюрата Albrehta Dyurera "Меланхолия I», се смята за най-ранните в европейското изкуство. Две средни числа в най-долния ред посочват датата на създаването на картината (1514).

Магически квадрат от 4 × 4, изобразен на гравюрата Albrehta Dyurera "Меланхолия I», се смята за най-ранните в европейското изкуство.

Сума от числата във всяка хоризонтална, вертикална и диагонална равен на 34. Тази сума също се намира във всички краища на квадрата 2 х 2 в централен квадратен (10 + 11 + 6 + 7), на квадрата на ъглови клетки (16 + 13 + 4 + 1 ) в квадрати конструирана "люлка кон" (2 + 8 + 9 + 15 и 3 + 5 + 12 + 14), в правоъгълници, образувани от двойки вторични клетки от двете страни на (3 + 2 + 15 + 14 и 5 + 8 + 9 + 12). Повечето от допълнителни симетриите, свързани с факта, че сумата на всеки два централно разположени симетрично числа е равно на 17.

подход по шахмат. Известно е, че шах, както и магически квадрати, имаше десетки преди векове в Индия. Затова не е случайно, че идеята за разсрочено подход към изграждането на магически квадрати. За първи път тази идея бе изразено от Ойлер. Той се опита да се възползвате от пълната магически квадрат непрекъснато байпас коня. Въпреки това, за да направите това той се провали, тъй като основна диагонали сумата от числата се различава от магия константа. Въпреки шах разбивка ви позволява да създавате всякакви магически квадрат. Цифрите са пълни редовно по ред въз основа на цвета на клетките.

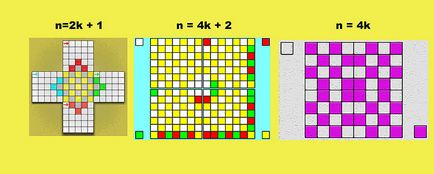
Изображение вериги изграждане магически квадрати.

Магически квадрати различни приписват мистични свойства. През 16-ти век. Корнелий Агрипа Хайнрих построена площади трета, четвърта, 5-ти, 6-ти, 7-ми, 8-ми и 9-ти поръчки, които са били свързани с астрология 7 планети. Общата вяра, че гравиран върху сребърна магия площада предпазва от чума. Дори и днес можете да видите на магически квадрати сред европейските астролозите атрибути.

Sudoku - вълшебната площада

Фенове на магически квадрати предлагат се отпуснете и да играят на игра на судоку. Sudoku - пъзел с числа пъзел, който е станал много популярен напоследък. Преведено от японски "су" - "цифра", "акостира" - ". Застанал сам" Понякога судоку нарича "магически квадрат". игралното поле е квадрат на 9x9, разделен на по-малки квадрати със страна 3 клетки. По този начин, всички игралното поле се състои от 81 клетки. Някои от тях вече са в началото на играта има няколко (от 1 до 9). В зависимост от това колко клетки вече са запълнени, бетон судоку може да се обясни лесно или трудно.

Не, добре kakmozhnosdelatkvadrat 3 на 3 Разбирам: * 5 в центъра, тъй като тя не разполага с чифт. * 9, 8, 7 dozhnynahoditsya не на същата линия, защото sume всеки две от тях да се получи желания резултат, ако не и повече ... Тогава dostavittsifry интуитивен, не е трудно. С 4 4 и повече или по-малко ясно. Подадени 2 квадрата са много сходни. С Единствената разлика е, че числата в първата клетка в редиците, а във втория площада. Не виждам друга симетрия. Но 5,6,7,8,9 - това е нереално!