Най-голям общ делител

Ако естествено число се дели само от един и само по себе си, това се казва, че просто.

Всяко физическо номер винаги се дели на 1 и себе си.

Номер 2 - най-малкият брой премиер. Това е само още по-просто число, другите основни числа - странно.

Много прости числа, както и на първо място сред тях - броят 2. Въпреки това, има последната просто число. В "проучване" на секция можете да изтеглите таблицата на простите числа до 997.

Но много естествени числа се делят поравно и повече на други естествени числа.

• 12 е разделен на броя на 1. 2. 3. 4. в продължение на до 6. 12;
• 36 е разделен на броя на 1. 2. 3. за от 4 до 12 от 6 до 18 от 36.

Номерата за които броят е неделими (до 12 е 1, 2, 3, 4, 6 и 12) са делителите на номера.

Делител на естествените числа е - това е естествено число, която разделя на определен брой «а», без следа.

Natural номер, който има повече от два делителя се нарича съставно.

Моля, имайте предвид, че цифрите 12 и 36 имат общ делител. Това е число 1, 2, 3, 4, 6, 12. Най-големият от тези номера делители - 12.

Общ делител на две числа от данни «а» и «б» - е броя, с което двамата разделен без остатък от данни и «б» «по-».

Най-големият общ делител (ГРУ) на числеността на два данни «а» и «б» - е най-големият брой, че и двете числа «а» и «б» се делят без остатък.

Накратко най-голям общ делител на «а» и «б» е написано, както следва:

Пример: GCD (12; 36) = 12.

Разделители номера в запис решения са означени с буквата "D".

Числата 7 и 9 имат само един общ делител - номер 1. Тези числа се наричат ​​взаимно прости числа.

Взаимно прости числа - са естествени числа, които имат само един общ делител - 1. Техният брой е 1 ГРУ.

Как да намерите най-голям общ делител

За да намерите НОД на две или повече естествени числа трябва да:

1. разширени разделители номера на основните фактори;

Изчисленията удобни да пишат с помощта на вертикалната линия. Вляво от функциите първо напишете дивидент, нали - разделител. Освен това, в лявата колона, запишете стойността на лично.

Нека обясним примера веднага. Разлага на основните фактори на 28 и 64.

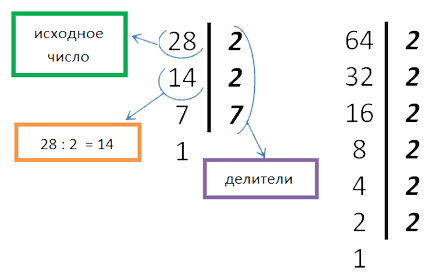
1. Ние наблягаме на същите простите множители и в двете числа.
   28 = 2 · 2 · 7

64 = 2 · 2 · 2 · 2 · 2 · 2

Ние намираме един и същ продукт от основните фактори и пише отговора;
GCD (28; 64) = 2 х 2 = 4

A: GCD (28; 64) = 4

Съдържание за намиране на НОД от двата начина: в колона (както направихме по-горе) или "в съответствие".

Първият метод за запис GCD

Намерете НОД на 48 и 36.

GCD (48; 36) = 2 · 2 · 3 = 12

метод GCD Вторият запис

Сега пиша разтвор GCD търсене на място. Намерете НОД на 10 и 15.

Можете също така на нашия уеб сайт на програмата с помощта на асистент, за да намерите най-голям общ делител онлайн. за да проверите своите изчисления.