научите да програмирате

Ако всички малолетни и непълнолетни matritsyAporyadkakravny нула, а след това всички малолетни и непълнолетни лица, за к + 1, ако те съществуват, също са равни на нула.
Рангът matritsyA нарича максимални непълнолетни лица ред на матрицата А. различна от нула.






Максимална ранг може да бъде равен на минималния брой редове или броя на колоните на матрицата, т.е. ако матрицата е с размер 4x5, максималната ранг ще бъде 4.
Най-малко с ранг на матрица е равен на 1, освен ако не се занимават с нулева матрица, винаги има ранг равен на нула.

Място поръчка квадратна матрица неособена матрица п е равно на N, тъй като той е непълнолетен определящ фактор за наш ред и неособена матрица матрица е различно от нула.
Транспонирането на матрицата не се променя нейното място в класацията.

Нека ранга на матрицата е. След това, всяка малка от ред, различен от нула, се нарича база непълнолетния.
Пример. Предвид матрица A.

Най-определящ фактор на матрицата е равна на нула.
Мала втори ред. Следователно, R (A) = 2 и второстепенния база.
Основа непълнолетен също е незначително.
Мала, защото = 0, така че ще има основен.
Задача. независимо провери какви други непълнолетни лица от втори ред са основни и кои не са.

Намирането на ранг на матрица чрез изчисляване на всички свои непълнолетни лица изисква твърде много изчислителна работа. (Читателят може да се провери, че в четвъртия ред квадратен матрица 36 непълнолетни, втори ред.) Ето защо, различен алгоритъм се използва за намиране на ранга. За да се опише тази нужда от допълнителна информация.

Ние наричаме тези стъпки елементарни матрици над тях:
1) прехвърляне на редове или колони;
2) умножаване на ред или колона на броя ненулеви;
3) добавяне на една от линиите на друг ред, умножена по броя на или добавянето на една от колоните на друга колона, умножени по брой.

Когато не елементарна матрица ранг се променя.
Алгоритъм за изчисляване на ранг на матрица, подобна на алгоритъм за изчисляване на определящ фактор, а е, че с помощта на елементарни матрица е сведена до проста форма, за които да се намери в ранг не е трудно. Тъй като за всеки ранг преобразуване не се променя, а след това, като се изчислява ранга на матрицата се трансформира, като по този начин ние се намери ранга на оригиналната матрица.

Да предположим, че искате да се изчисли ранга на размерите на матрицата мексикански песо.

1. С пермутация на редове и колони на стремежа да се гарантира, че в горния ляв ъгъл на матрицата е различна от нула елемент. Така че, ние вярваме, че. Първият ред оставяйки непроменена.
2. Вторият ред добавим първата, умножена по броя.
3. За да добавите третия ред на първия ред, умножен по броя.
4. Процесът продължава, докато, докато не се получи нула на първо място на последния ред. Резултатът е матрица от А1, където в първата колона всички елементи са 0 освен член.

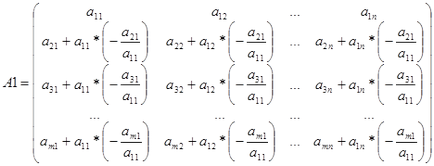
А1 изчисления матрица има формата

1. Ако всички редове, започвайки от второто, което води до нула матрица, а след това му ранг е равен на 1, тъй като има незначително първия ненулев ред. В противен случай пермутация на редове и колони с номера по-големи единици се постигне, че вторият елемент на втория ред е различна от нула. Така че, ние вярваме, че.
2. Първа и втора линия на резерва непроменен.
3. За да добавите третия ред на втората, умножена по броя. Резултатът е, че вторият елемент на третия ред е нула.
4. След това добавете четвъртата линия на втория, умножена по броя и т.н. Резултатът е матрица

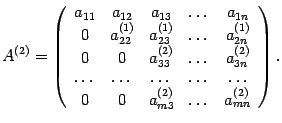
Ако всички редове от третия, нула, след като маловажен. В противен случай пермутация на редове и колони с номера по-големи от две, правят на третия елемент на третия ред е различна от нула. Освен това, добавянето на третия ред, умножена по съответния брой на редовете, за да се получи голям брой нули в третата колона от четвъртия елемент и т.н.
В един момент стигаме до матрица, при което всички линии се започва с (R + 1) тата. са нула (или отсъства в) и незначително в първия ред и първата колона е детерминантата на триъгълна матрица с ненулеви диагонални елементи. Рангът на матрица е равна. Следователно Rang (A) = R.

В предложения алгоритъм за намиране ранг на матрица всички изчисления трябва да се извършват без закръгляване. Произволно малка промяна в поне един от елементите на междинно съединение матрицата може да доведе до факта, че отговорът получен ще се различава от оригиналната матрица ранг в няколко единици.
Ако оригиналните матрични елементи са цели числа, след изчисляване е удобно извършва без използване на фракции. Поради това, на всеки етап е препоръчително да се умножи броя на линиите, така че, когато изчисленията на фракциите не се срещат.

В лабораторни и практическа работа, помислете за пример, когато един ранг на матрица.

Алгоритъмът за намиране на матрица норма.
Разпределяне на само три матрица норма.
Първата матрица норма = максимум цифрите, получени при добавянето на всички елементи на всяка колона, взети модул.
Пример: Нека 3x2 матрица даден размер (Фигура 10). В първата колона са елементи 8, 3, 8. Всички компоненти са положителни. Намираме сумата им: 8 + 3 + 8 = 19. Във втората колона са елементи 8, -2, -8. Два елемента - отрицателни, така че добавянето на тези цифри, е необходимо да се замени модул тези числа (т.е. без "минус" знак). Намираме тяхната сума: 8 + 2 + 8 = 18. Максималният размер на две числа - е 19. Така че първото правило на матрицата е равна на 19.

Второто правило на матрицата е квадратен корен на сбора от квадратите на всички елементи на матрицата. И това означава, че ние квадратура всички елементи на матрицата и след това да добавите до стойностите, получени от резултатите от корен квадратен.
В нашия случай, 2 матрични норми са равни на корен квадратен от 269. На диаграмата, аз научих приблизително корен квадратен от 269, и в резултат получи приблизително около 16,401. Въпреки, че по-правилно да не се извлече корен.

Една трета норма на матрицата е големият брой, получен чрез добавяне на елементи от всеки ред, взети модул.
В нашия пример на първия ред елементи са: 8 8. Всички положителни елементи. Ще се намери сумата им: 8 + 8 = 16. Във втория ред елементи са: 3, -2. Един от елементите е отрицателен, така че добавянето на тези цифри, е необходимо да се замести модул този номер. Намираме тяхната сума: 3 + 2 = 5. Третият ред стоят елементи 8 и -8. Един от елементите е отрицателен, така че добавянето на тези цифри, е необходимо да се замести модул този номер. Ще се намери сумата им: 8 + 8 = 16. Максимумът на тези три числа - е 16. Така че третата норма на матрица е равна на 16.

Съставител Saliy NA