Общи и проба на населението - studopediya

Математическа статистика - наука, която, въз основа на методите на теорията на вероятностите, се занимава с систематизирането и обработката на статистически данни за научни и практически изводи.

Статистическите данни, посочени данни за броя на обектите с тези или други атрибути.

Група обекти, обединени от някаква качествена и количествена черта, наречени статистическата съвкупност. Обектите, включени в съвкупността, се наричат ​​неговите елементи, както и общият им брой - обема.

Общото население е съвкупност от всички възможни евентуални наблюдения, които биха могли да бъдат направени най дадена реална или сложни условия по-отблизо: населението се нарича случайна променлива х и свързаната вероятност пространство.

Разпределението на случайна променлива х се нарича разпределение на населението (например, например, нормално разпределение или общото население нормален).

Например, ако броят на независими измервания направени на случайна променлива х, общото население е теоретично безкраен (общото население т.е. - абстрактно условно - математически концепция); ако се проверява броят на дефектните елементи по партидата на N предмети, а след това тази игра се счита за крайния обем на общото население N.

Ако броят на обектите N е достатъчно голяма, че е трудно да се проведе преброяване на населението, а понякога и физически невъзможно (например, за да се провери качеството на всички кръгове). След това, избрани на случаен принцип от цялата популация ограничен брой обекти и се подлага на тяхното изследване.

Общата проба или проба от размер п е X1 последователности. x2. ..., Xn от независими идентично разпределени случайни величини, разпределението на всяка от които съвпада с разпределението на случайна променлива х.

Например, п от първите случайни променливи измерванията х обикновено се разглежда като проба от безкраен обем п в населението. Получените данни се нарича наблюдение случайна променлива х, а също така се казва, че случайна променлива х "е на стойност" X1. x2. ... хп.

Основната задача на математическата статистика - да се направи, основани на доказателства изводи за разпределение на едно или повече неизвестни случайни величини и отношенията им един към друг. Методът се състои в това, че въз основа на свойствата и характеристиките на извадката, за да се направят изводи относно характеристиките и числовите стойности случаен закон за разпределение (населението) се нарича метод за вземане на проби.

За характеристики произволни стойност, получени по метода на вземане на проби, бяха цел, е необходимо, че пробата е представителна, т.е. доста добре представени изследвана стойност. Законът за големите числа може да се твърди, че извадката е представителна, ако то се осъществява на случаен принцип, т.е. всички обекти от общото население имат еднаква вероятност да бъдат взети проби. Съществуват различни видове за подбор на извадката.

1. Един прост случаен подбор се нарича избор, където обектите се изтеглят една по една от цялото население.

2. Стратифициран (стратифицирана) подбор се крие във факта, че първоначалната обща структура по обем е разделена на подгрупи N (страта) N1. N2, ..., Nk. така че N1 + N2 + ... + Nk = Н. Когато бразди определят от всяка от тези екстрахира проста произволна проба с размер n1. n2. ..., НК. Специален случай на стратифицирана вземане на проби е типичен избор, където избраните обекти не са от цялото население, и всеки един от типичните част.

Комбиниран избор комбинира няколко вида избор, образувайки различни проучване фаза проба. Има и други методи за дизайн проба.

Пробата се нарича отново, ако избрания обект на избора на следващия връща на населението като цяло. Пробата се нарича четене веднъж, ако избрания обект в общата популация не се възстановява. За крайната общото население на случайна извадка, без подмяна на всяка стъпка води до зависимост между отделните наблюдения, принципа на случайния подбор еднакво вероятно да се върне - да наблюденията са независими. На практика обикновено се справят с повторение без проби. Въпреки това, когато размерът на населението п е много пъти по-голям от размера на п на пробата (например, стотици или хиляди пъти), при спазване зависимост може да се пренебрегне.

Така произволна проба x1. x2. ..., Xn - е резултат от последователни и независими наблюдения на случайна променлива ξ, представляващи населението като цяло, както и всички елементи имат същото разпределение за вземане на проби, че първоначалната случайна променлива х.

Fx на разпределителна функция (х), и други количествени характеристики на случайни променливи X ще се нарича теоретично, за разлика от характеристиките на пробите. които се определят въз основа на резултатите от наблюденията.

Нека x1 на извадката. x2. ..., ХК е резултат от независими наблюдения на случайни променливи х, и x1 наблюдава n1 пъти х2 - N2 пъти, ..., XK - NK пъти, така че Ni = N - размер на пробата. Ni номера. което показва, колко пъти се появява XI стойността на п наблюдения се нарича честота на стойностите и Ni съотношението / п = Wi - относителната честота. Очевидно е, че броят на Wi и рационално.

Статистическа жители, разположен в възходящ ред на функция, наречена вариационен серия. Нейните членове представляват х (1). х (2), ... х (п) и наречени изпълнения. Вариант номер се нарича дискретно. ако членовете му вземат конкретни изолирани ценности. Статистическа извадка разпределението на дискретна случайна променлива х е списъкът опция и съответната относителна честота Wi. Получената маса се нарича статистическите редове.

Фиг. 7.1.3 и 7.1.4, конструирана съгласно таблица 7.1.2, представена хистограма и кумулативна честота графика. Кривите съответстват на плътността на функцията за нормално разпределение, "съвпадение" на данните.

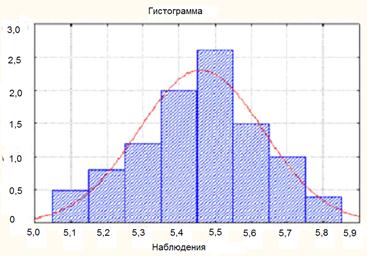
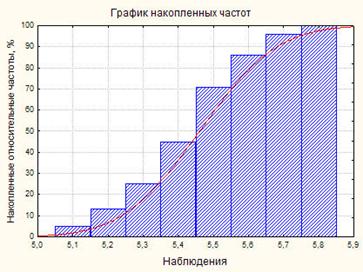
По този начин, разпределението на извадката е разпределение приближение на населението.