Паралелизъм на линия и равнина и две равнини - паралелност и перпендикулярност на линията и
92 *. Чрез точка А до заема линия, успоредна на равнината на триъгълник BCD (фиг. 90, както и).
Решение. Direct, успоредна на равнината, ако тя е успоредна на който и да е права линия лежи в равнината. Поради това, през точка А може да се направи неопределен брой паралелни линии на даден самолет. Например, разходите (фиг. 90, б)
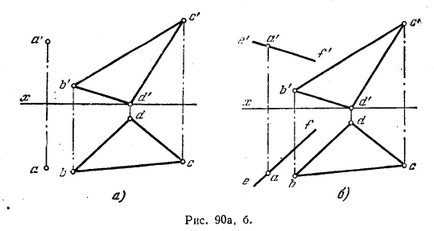
през точката за "директни e'f" паралелно B'D "и по линия, успоредна направо BD де, ние получаваме проекция EF линия, успоредна на страна на СД на триъгълника, а оттам и неговата равнина. Избор на линия BD е произволна.
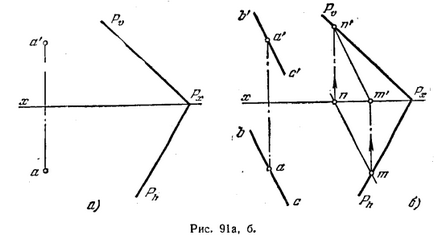
93 *. Чрез точка А до точка заема линия, успоредна на Пл. F (фиг. 91).
Решение. Построява (фиг. 91.6) и m'n прогнозния млн "права линия MN, лежащ в квадрат. Р. След това, след като "държи фронта. проекция Б "паралелна m'n"
и с хоризонт. бв успоредна проекция млн. Пряка слънчева успоредно MN линия, а оттам и на равнината P.
94 *. За да се определи дали една линия AB е успоредна на равнината Р (Фиг. 92 А).
Решение. За да се определи дали успоредна линия AB депутат. P, е необходимо да се опита да извърши в тази равнина права линия успоредна на тази. Фиг. 92, се извършва втора отпред. проекция C'D "паралелна A'B". Изграждане на хоризонт. CD проекция.
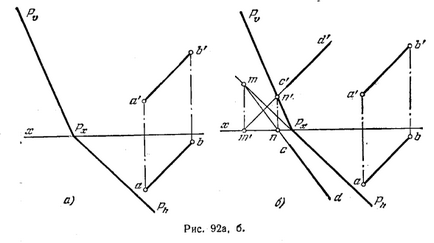
при спазване на условието, че CD на линията трябва да бъде на площада. P. Тъй изграждане издатини CD не е успоредна на AB, след това линиите АВ и CD не са успоредни и това означава, че линията AB и квадрат. P също не е успоредна.
Можете да започнете с хоризонт. проекция на линия, паралелна направо на АВ, изграждане на предната. проекция, придържайки се към условията, които тази линия трябва да са на площада. P, конструирана и спрямо предната част. проекция с A'B ".
95. Определете дали е успоредна на линията AB
а) равнина, определена от паралелни линии CD и EF (фиг. 93 а)

б) равнина Р (фиг. 93 б),
а) Q равнина (фиг. 93 С).
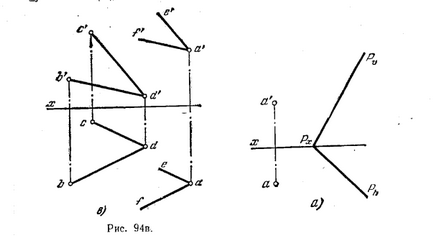
96 *. Чрез точката равнина, успоредна на равнината, определена от точки В, С и D (фиг. 94 А).
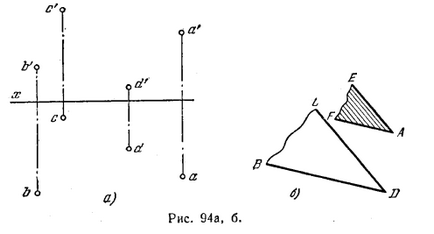
Решение. Две равнини са успоредни, ако две пресичащи се линии на един от тях, съответно, успоредни на две пресичащи се прави линии различна равнина (фиг. 94, б).
За да се конструира желаната равнина прекарват в дадена равнина две пресичащи се прави линии BD и CD (фиг. 94, В и С). След това, чрез "държи a'f" паралелна b'd "и" д ", паралелно s'd", а чрез паралелен холдинг ае BD и CD ад паралелно Direct AR и AE, паралелни BD и CD, като по този начин, са успоредни и равнината, определена от тях.
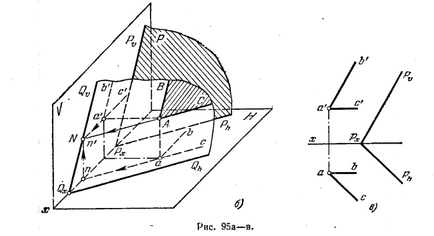
97 *. Чрез точка А (фиг. 95 а) Към равнина, успоредна на топене. Р.
Решение. Както е известно, хоризонтални паралелни равнини, успоредни една на друга, паралелни един на друг и предна. Също така, следи от същото име паралелни равнини, съответно успоредни една на друга (фиг. 95 б).
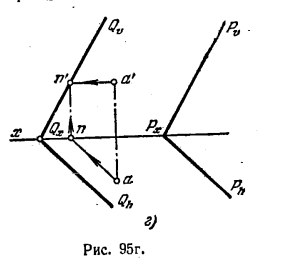
Фиг. 95, и дава желаната равнина от две прави хоризонтална предна AB и AC, което чрез "държи A'B" паралелна Pϑ и а'с "успоредна на оста х и през точката и паралелно провеждане АС и аб Ph, успоредна на оста х. Тъй като следа от Pϑ Той е един от фронталния площада. P, и рН на следа - един от нейните контури, ние получаваме паралелно контура и паралелно челен една и друга плоскост, т.е. успоредно на тези самолети ... Фиг. 95 грама илюстрира структурата на желаната равнина на своята следи Qϑ и Qh. За изграждането им направи през точка А хоризонтална равнина, успоредна до желаната песен и да намерят Ph отпред. проследяване N (N, N ') на тази хоризонтална линия. Сега чрез енд кери Qϑ || Pϑ Qx намерите точка на оста х и направи пътека успоредно Qh Ph
98. След точка А (Фигура 96) Към равнина, успоредна на равнината, определена от паралелни линии CD и EF; експресират желания равнина от две пресичащи се линии.
99. След точка А (фиг. 97) да равнина, успоредна на MP. P; експресират желания равнината на релсите.
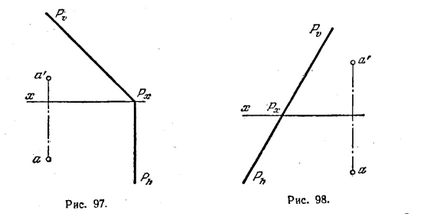
100. След точка А (фиг. 98) да равнина, успоредна на MP. Р. Дайте отговори: а) изрази пл. Фронтале хоризонтална п, б) проследява.
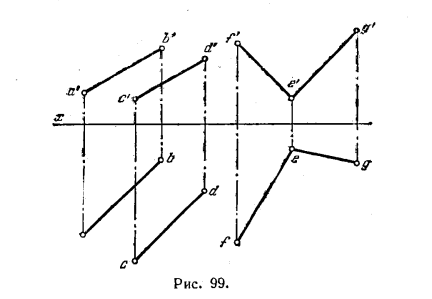
101. За да се определи дали равнина, един от които е определен успоредни линии АВ и CD и други паралелни - пресичащи се линии EF и EG (Фигура 99).