Прекрасна Блез Паскал триъгълник, математика, което ми харесва
Всички знаем за триъгълник на Паскал в младежките си години. Но, очевидно, не знам всички чудеса, които съдържа триъгълник. В действителност, ние все още се откриват нови неща!
Конструиран триъгълник е доста лесно: на външните краища трябва да поставите модула, като всеки брой вътре е сумата от двете числа, които стоят над него. По този начин, третото число в шестия ред е, защото това е сумата от цифрите и.
Внимание! В действителност, ние казваме, че е вторият по брой на петия ред. По причини, които скоро ще станат ясни, ние започваме да преброят редовете и колоните на триъгълник от нулата. Например, второто число е равно на четвъртия ред.
Знаейки правилото за допълнение, е безкраен: можете да напишете колкото се може повече линии, както търпението ще позволят.
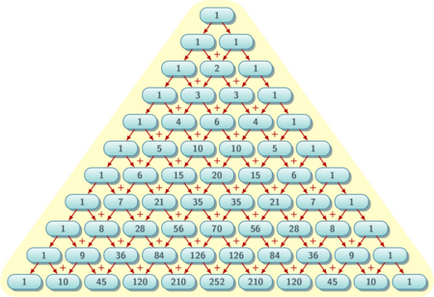
Първите 10 редовете на триъгълника на Паскал
Паскал въведена триъгълник си в 1653 в Traité дю триъгълник arithmétique като част от изследването на вероятностите и компютри. Задачи са приблизително по следния начин: "Ако искам да избере двама души от данните, четири, тъй като има възможни двойки '' или" Каква е вероятността за получаване на пълна къща Когато получава по пет карти (забележка покер три карти от един ранг и две от друг.) от палубата, което е добре смесена? "Паскал и Ферма главно обсъжда вероятността от писма, те обменят по това време. Можете да видите източника на триъгълник на Паскал тук.
Как триъгълника е свързан с вероятността? Е, ако искате да изберете обекти от базата данни, броят на възможните решения е равен на броя на ти-ти ред на триъгълника. Не забравяйте, че низове и числа числа в линиите на триъгълник започват от нулата! Използването на това правило, ще видим, че има точно два начина за избор на лице на данните четири. И така - третото число в деветия линия на триъгълника, тогава няма начин да се избере три от девет данни. Научете се как да го изчисли, можете да направите една малка стъпка за изчисляване на различни вероятности.
На пръв поглед изглежда съвсем ясно защо триъгълника дава правилния отговор на този въпрос. Тя може също да изглежда странно, че винаги трябва да се започне от нулата, за да се заемем с работата. За да се види, че всичко това е напълно вярно, ние ще направим два коментара.
На първо място, ако имате група от обекти, колко много начини можете да изберете нула предмети от тях? Има точно един начин да се избере нула обект, а именно, просто заявява, че не вземете някоя от тях. Освен това, имате само един начин да изберете всички обекти. Това отговаря точно на звената в двата края на всеки ред.

На второ място, ако искаме да изберете обекти от данните, забелязваме, че има две взаимно изключващи се сценарии: или любимата ни тема е един от кандидатите, или не е. Ако можем да го изберете, ние също трябва да изберете обекта на останалите елементи, за да изберете точно предмети. Ако не изберете този въпрос, ние трябва да изберете всички елементи от субекта на данните, оставаща след изключването на любимата ни тема. Тъй като това е взаимно изключващи възможност да получите от общия брой на избор, ние трябва да се определя броят на опциите във всеки сценарий.
С една дума, за да получите няколко начина за избор на обекти от базата данни, трябва да се определят броя на начина за избор на обект на, както и броя на начина за избор на обекти от. Но точно това е правилото за допълнение на триъгълник на Паскал!
Вече знаем, че триъгълника е напълно определя от местоположението на блокове в своите страни, а правилото за допълнение. Тъй като тези свойства са приложими и за отговора на въпроса за броя на обекти на избори, и на триъгълника трябва да даде правилния отговор тук.
Възможност да правите тези изчисления е безценно в много случаи. Ето защо, малко изненадан, че Паскал не е първият. Тези числа се считат за индийски, китайски и ирански математици по различно време, като се започне от момента на повече от хиляда години. И, разбира се, всеки ще знае триъгълника Яна Hueya, 1303 гр.:
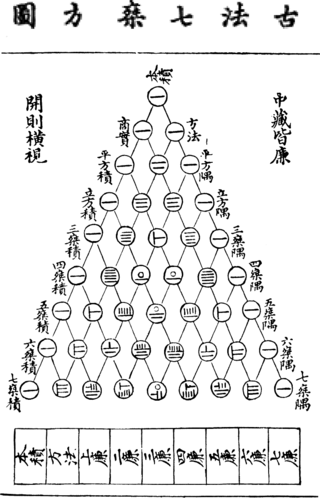
По ирония на съдбата, дори и без да може да се направи разграничение на броя, можете да намерите на печатна грешка в този триъгълник, който е повече от 700 години! Съвет: За да добавите правило се триъгълник на Паскал е симетрично по отношение на вертикалната линия, минаваща през неговия връх. Ако се вгледате внимателно, в триъгълника на Ян Hueya, тази симетрия е счупен на едно място.
В триъгълник, много прекрасно. Къде са чудесата? Някои от тях са лесни за място. Ако добавите номера в I-ред на триъгълника, винаги ще получите в степента (например). За нас, това е доста скучно.
Малко по-интересен е фактът, че ако добавите до броя на стоящи в триъгълник по диагонала, можете да получите поредица от числата на Фибоначи. А Фибоначи самата последователност съдържа много изненади.

Нека да обозначи произведението на цифрите в I-ред на триъгълника. Така че, и така нататък. Номерата, които са получени, не изглежда да има никакви видими чудодейни свойства. Ние Brothers са имали идеята да види какво ще се случи, ако се раздели на тези продукти, изчислени за съседните редове. По-точно, това е установено, че броят получен чрез следната формула:
. Това е, за всеки ред, той смята фракцията, чийто числител е продукт на всички числа в ред, който стои под него, и в един ред, който стои над нея, а знаменателят - продуктът на всички числа в този ред на площада.
И удивителното: когато става все повече и повече, това съотношение е все по-близо до броя! Не забравяйте - това е десетично число с безкраен брой цифри, което е приблизително равен. Тя се появява, когато капитализирането на лихви, броят на моделите на растеж на населението и други ситуации, с експоненциален растеж. Учудващо е, че този брой може да се окаже доста прост процес, намерени в триъгълник на Паскал. Е, как да знаете какво да търсите, не е лесно да се разбере, че прегледът на отношенията наистина е все по-близо до растеж. Както можете да видите тук. за изчисляване изисква само малко алгебра.
Това е такъв сладък анимация Richarda Grina показва резултатът от Harlan Brothers:
Има още едно чудо в триъгълника, които всеки трябва да знае. Нека броят на всеки триъгълник на цвят в един от двата цвята, в зависимост от това дали е дори и странно. Например, ние може да рисувам четни бяло и странно - синьо. Ако правим това за първите 500 линии на триъгълник, тук получаваме модел:

Той е известен фрактал известен като Sierpinski триъгълник! Това води до най-различни въпроси. Броят е дори или нечетен, ако е на разделяне, като остатък или съответно. Какво се случва, когато се разделят на? Остатъците могат да бъдат равни на или по-малко. Какво се случва, ако използваме осем цвята и оцвети всеки номер в съответствие със своята остатък, когато разделена на осем? За първите 500 линии на триъгълник получаваме красива картина:

Налице е забавно малко приложение. който ви позволява да видите какво се случва, ако промените броя, с което споделяте (наричани също модули). Съвет: Когато използвате приложението, кликнете върху малката символа "плюс" ", за да се използва по-подробна версия на контрола. В триъгълник на Паскал има много други невероятни неща. За начало, ако се интересувате от това, подходящ уебсайт mathforum.org. Но повече от, да речем, ексцентричен, неща, които могат да бъдат намерени в триъгълника, има тук.
Гафове - абсурди, извършени предци и нас
2 VF Korneyev.:
И как ти харесва простотата на следните критерии:
номер, ако и само ако прост, когато всички триъгълник на Паскал (единица не се брои) с номера на реда на числата се делят на този номер.
От 9 не е отличен, защото 84 не се дели на 9. 7 - просто, защото всички от седмия ред е разделен на седем.
Някак си твърде очевидно се оказа. )
Всяка число куб poetomu10st.3n = 500 х 10 член 3 (п-1) + 500 x10st.3 (п-1), където 500 х 103 (М-1) от нечетен и дори повече. Целите числа, започващи с една и техните номера с 0.
Мурад, много интересни изводи и аргументи. но това не е ясно. Бих искал да науча повече