Примери за решаване на проблеми - studopediya
Пример 1. Определяне на потенциала йонизация и първата потенциал възбуждане водороден атом.
Йонизация потенциал Ui нарича най-ниската потенциална разлика, че трябва да премине през електрон ускоряване поле за сблъсъка с спокоен глас атом го йонизира. Работа за отстраняване на електрона от атом, Ai е електрически напрегнатостта на полето, който ускорява електрона, EUI. Следователно, Ai = EUI.
Като се има предвид естеството на квантовата поглъщане на енергия от атома, можем да кажем, че работата на йонизация Ai е квант енергия ВН. абсорбира водороден атом при прехода на електрон от първия Бор орбита в орбита в безкрайността. След прилагане на серия формули на Balmer и пускането n1 = 1; 2 = ∞, получаваме:
.
;
.
Първият възбуждане потенциал U1 имат най-нисък потенциал разликата, която ще се проведе в ускоряване областта на електрон към сблъсък с спокоен глас атом го прехвърли на първо възбудено състояние. За водород, това отговаря на електрон преход от първата към втората Бор орбита. Приравняването на работната сила ускоряване електрическо поле ЕС1 квантова енергия ч # 957;. атомноабсорбционна по време на преход към първото възбудено състояние, получаваме:
,
.
.
Пример 2. електрон начална скорост, която може да бъде игнориран е преминал ускоряване на потенциалната разлика U. Определя де Broglie дължина на вълната на електрон в два случая: 1) U1 = 51 V; 2) U2 = 510 кВ.
тр. млн и Mya - съответно протон маса, неутрони и ядро.
маси поглед нагоре винаги са дадени маса на неутрални атоми, но не ядра, така формула (1) е целесъобразно да се превърне, така че да включва тегло М неутрален атом. неутрална атомна маса равна на масата на ядрото и електроните, съставляващи електрони обвивка на атома: ma = Mya + Zme. където Mya = ma - Zme. Тогава формула (1) е под формата:
.
Отбелязва, че т.т. + ме = (маса на водороден атом), накрая получаване на:
.
Заместването в този израз цифровите стойности на масите в атомни масови единици (Виж Таблица 15 и Приложение 17 ..), получаваме:
За изчисляване на ядрената задължителен потребление на енергия формула
ЕЬ = 931 х 0,04216 MeV = 39,2 MeV.
Пример 7. При сблъскване # 945; -частици с борен ядро на ядрената реакция настъпили, което води до две нови ядра са се образували. Един от тези ядра беше ядрото водороден атом. Определя се броят на последователност и масовото число на втория сърцевината, запис реакция енергия символично ядрената и се определя ефект.
Означаваме символ неизвестен ядро. защото # 945; -particle е хелий ядро. записване на реакцията:
.
Прилагането на закона за запазване на заряда, получаваме уравнението: 2 + 1 = 5 + Z. където Z = 6. Прилагането на закона за запазване на нуклоните, ние получаваме уравнението: 4 + 10 = 1 + А. където А = 13. Следователно, неизвестен ядро е в основата на изотоп въглероден атом. Сега можем да си запишете ядрената реакция в окончателния си вид:
.
Q енергичен ефект на ядрената реакция се определя от формулата:
Смяна на първоначалната маса на реакционните ядра и ядра тегло продукти на масите на неутрални атоми (. Таблица 15 виж допълнение) и ги заместване на формулата за изчисление, ние получаваме:
Q = 931 [4.00260 + 10.01294) - (+ 13.00335 1.00783)] = 4.06 MeV MeV.
Отговор: Q = 4,06 MeV.
Пример 8. Определяне на реакционната енергия 10 V (п, # 945) 7 Ли. произтичащи от взаимодействието на неутрони с много бавни покой борни ядра. Намери и кинетичната енергия на продуктите на реакцията.
В ядрената реакция 10 (п, # 945) 7 Li е както следва. бор ядро. абсорбиращ бавно неутрони. превърнато в междинно съединение ядро. Последните, ентусиазиран, излъчва # 945; -particle (т.е. хелий ядро), се превръща в литиев ядро. В разгънатата формата на реакцията е написано, както следва:
.
Енергия ядрена реакция (или топлината от реакцията) Q се определя от формулата:
Смяна на масата на атомните ядра атоми се опират маси почивка (.. Виж Таблица 15, допълнение) получаваме:
- 4,00260) = MeV 2.8 MeV.
За кинетичната енергия на реакционните продукти - литий 7 ядрата и Li # 945; -частици, се прилага законът за запазване на енергията и релативистката инерция опазване закон:
;
като се вземат предвид уравнението (1) получаваме:
От условията на проблема, от това следва, че стойностите на TB и Tn могат да бъдат пренебрегвани. След това стигаме до сумата от кинетичната енергия на частиците 7 Ли и 4 Той:
Според закона за запазване на инерцията :.
Ако приемем, че общата инерция на частиците на реакцията е нула, ние получаваме:
.
Следователно, за модули импулсни имат :.
Бобови частици и тяхната кинетична енергия са свързани. Ето защо:
Решаването на системата от уравнения (2) и (3):
.
.
.
Пример 9. Positron с кинетична енергия T = 0.75 MeV инцидент на покой свободен електрон. В резултат на това има два унищожение # 947; фотон със същата енергия. Определяне на ъгъла # 952; между посоките на експанзия.
Т = 0.75 MeV = 0.75 х 1.6 х 10 -13 J m0 = 9,1 х 10 -31 кг е1 = е2 = д
Метод унищожение електрон е - и д + позитрон настъпва схема е - + д + → # 947 + # 947; и се подчинява
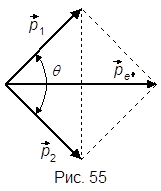
В същото време. където # 949; - енергията на всеки # 947; -photon.
От фигура 55 получаваме. след това:
(*)
За да се изчисли ъгъла # 952;. е необходимо да се определи инерцията и енергията на позитрона # 949; всеки # 947; -photon. Импулс позитрон намери знае своята кинетична енергия Т. Тъй като стойността на Т надвишава енергията на позитрон m0c 2 = 0,511 MeV почивка, позитрон следва да се разглежда като релативистично частиците. В този случай се използва инерцията на частицата се изразява с формулата.
енергия # 947; -photon # 949; определя с използване на закона за запазване на енергията релативистичната:
,
където - сумата на енергиите на частиците към останалата част от реакционната смес, и - сумата от техните кинетични енергии. Вдясно са количествата, свързани с частиците след реакцията. Като се има предвид, че масата на фотона е нула почивка :. и общата енергия на фотоните имат кинетична енергия, т.е. , и електрона и позитрона имат една и съща маса m0 останалите. Ние се получи.
Заместването в уравнение (*), # 2 стойност 949, и стойността на импулс позитрон. намерите:
.
Тъй като енергията на електрон останалите (позитрон) m0c 2 = 0,511 MeV, ние получаваме:
; ,