Радиан и степен мярка на ъгъла
Тук ние ще обсъдим въпроса Proc32 - Proc33 на Taskbook Абрахамян: описанието на ъгли на функциите на преобразуване от градуса в радиани и обратно.
Така че това, което е най-Радиан мярка за ъгъл? Да разгледаме окръжност с радиус R, съсредоточен на О. От кръга е разделен на 360 градуса и периферната дължина 2πR, след това 1 градус дължина дъга равен 2πR / 360 = πR / 180. След това ъгълът α градуса съответства на L дължина дъга = πRα / 180.
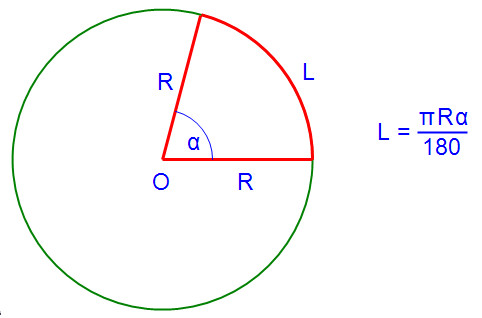
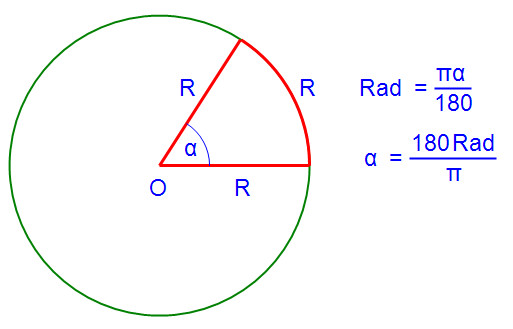
В този смисъл, ситуацията е много интересно, когато дължината на дъгата L е равно на радиус R. кръга Какво с ъгъл на дъгата? Припомня предишната формула за изчисляване на дължината на дъгата, имаме: πRα / 180 = R, където πα / 180 = 1, и ние получаваме α = 180 / π.
По този начин, ако дължината на дъгата е равен на радиуса на кръга, съответния ъгъл е 180 / π. Този ъгъл се нарича радиан (Rad):
1 Rad = 180 / π градуса.
пи радиана = 180 ° и 1 ° = пи / 180 радиани.
Радиан мярка на ъгъла - това е такава мярка на ъгъла, под който получи 1 Rad ъгъл на дъга, равна на радиуса на дъгата. От 1 радиан съответства на дължината на дъга, равна на радиуса, това означава следното заключение:
Големината на радиан мярката на ъгъл е равен на съотношението между дъгата и радиуса на този кръг.
Например, ако дължината на дъгата е равна 1.5R, на радиан мярка на ъгъла на дъгата е равна на 1.5; Ако дължината на дъга е равна на 0.25R, Радиан мярка, равна на 0,25; дължина на дъгата 2pR (цялата обиколка) Радиан мярка е равен на 2π, и т.н. Обикновено дължината на дъгата L на ъгъла в радиани е равно на L / R, където R - радиус.
Радиан - е един много удобен начин за измерване на ъгли, защото вместо самите ъгли, ние може да работи с съотношения на дължини на дъги и радиуси. В висша математика само Радиан мярка използва във всички тригонометрични функции.
Proc32. Опишете функция DegToRad (D) от материал, който връща стойността на ъгъла в радиани, ако нейната величина се дава в градуси D (D - реално число, 0 ≤ D <360). Воспользоваться следующим соотношением: 180° = π радианов. В качестве значения π использовать 3.14. С помощью функции DegToRad перевести из градусов в радианы пять данных углов.