равнобедрен триъгълник
предназначение
• Да запознае студентите с равнобедрен триъгълник;
• Продължете да формират умения за изграждане на ъглови триъгълници;
• Повишаване на знанията на учениците за свойствата на равнобедрен триъгълник;
• Фиксирайте теоретичните знания за решаване на проблемите.
цели на урока
• За да бъде в състояние да формулира, да докаже и да използват теореми от свойствата на равнобедрен триъгълник в процеса на решаване на проблеми;
• Продължаване на развитието на съзнателно възприемане на учебния материал, логическо мислене, самонаблюдение и умения за самооценка;
• Обадете се на когнитивната интерес към уроците по математика;
• Обучение на дейност, любопитство и организация.
план урок
1. Общи понятия и определения на равнобедрен триъгълник.
2. Свойства на равнобедрен триъгълник.
3. Признаци на равнобедрен триъгълник.
4. Въпроси и задачи.
равнобедрен триъгълник
Равнобедрен триъгълник - триъгълник има две равни страни, които се наричат страните на равнобедрен триъгълник, както и на третия партия, наречена основата.
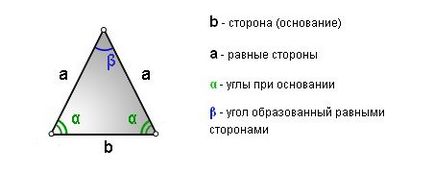
Върхът на тази цифра е това, което е в предната част на основата му.
Ъгълът, който се намира точно срещу база се нарича ъгъл на върха на този триъгълник, а другите две се наричат ъглови ъгли в основата на равнобедрен триъгълник.
Видове равнобедрен триъгълник
Равнобедрен триъгълник, както и други фигури могат да имат различни мнения. Сред остроъгълен равнобедрен триъгълник отговарят, правоъгълна, тъп и равностранен.
• остър триъгълник има всички ъгли остри.
• Y правоъгълен триъгълник върховете на прав ъгъл и остри ъгли, разположени в основата.
• тъп тъп ъгъл има един връх, а в основата му ъгли са остри.
• Направете равностранен всички негови ъгли и страни са равни.
Свойства на равнобедрен триъгълник
• срещуположни ъгли по отношение на равните страни на равнобедрен триъгълник са равни;
• ъглополовящи, медиани и височина, проведени от ъгли точно срещу равни страни на триъгълника са равни.
• ъглополовяща, медиана и височина, режисиран и провежда на основата на триъгълника съвпада с един от друг.
• центрове на вписаните и окръжности лежат на височината, ъглополовящата и медианата (те съвпадат), проведено на земята.
• Противопоставяне на равни страни на равнобедрен триъгълник ъгли, винаги остър.
Тези свойства на равнобедрен триъгълник се използват при решаването на проблемите.
домашна работа
1. Дайте определение на равнобедрен триъгълник.
2. Каква е спецификата на тази триъгълник?
3. Каква е разликата от триъгълник правоъгълен равнобедрен?
4. Какво познати свойства на равнобедрен триъгълник.
5. Какво мислите, възможно ли е на практика да се провери равенство на ъглите в основата и как да го направя?
А сега нека да има малко по-викторина и разберете как можете хванете нов материал.
Слушайте внимателно и да отговори на въпросите дали това твърдение е вярно, че:
1. триъгълник може да се разглежда като равнобедрен, ако е две страни са равни?
2. ъглополовяща се нарича сегмент, който свързва върха на триъгълника със средата на противоположната страна?
3. ъглополовящата на отсечка, която разделя ъгъл, която свързва горната част на обратната страна на точката на половина?
Съвети за решаване на проблемите на равностранен триъгълник:
1. За да се определят периметъра на дължина равнобедрен триъгълник страна, достатъчно да се умножава по 2 и се добавя тази работа с триъгълни бази в дължина.
2. Ако проблемът известен периметър и дължината на равнобедрен триъгълник бази, а след това да се намери дължината на страната на бази е достатъчно, за да отнемат от дължината на периметъра и намери, разделено на 2 разликата.
3. И, за да открие дължината на основите на равнобедрен триъгълник, и знаейки, периметъра и дължината на страната, е необходимо само да се размножават на страната на две и се изважда този продукт от нашия периметър на триъгълника.
1. Сред триъгълници на фигурата се определят едно допълнително, и да обясни избора си:
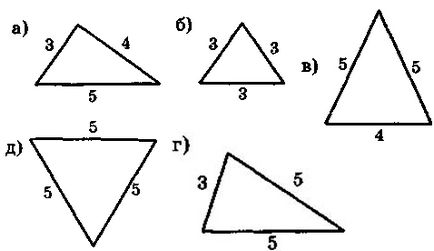
2. определи кои от триъгълници, изобразени на Фиг са равнобедрен, името им база и страни, както и изчисляване на техния периметър.
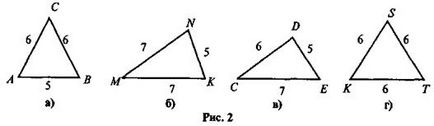
3. Периметърът на равнобедрен триъгълник е 21 см. Намерете страните на този триъгълник, ако един от тях е повече от 3 см. Колко решения могат да имат тази задача?
4. Известно е, че ако страничната страна и срещуположната ъгъл на базата на един от равнобедрен триъгълник е равна на крило и ъгъл от друга страна, тези триъгълници са равни. Докажете това твърдение.
6. Ако страните равнобедрен триъгълник са равни на 4 m и 5 m, което е периметъра си? Колко решения може да има този проблем?
7. Ако един от ъглите на равнобедрен триъгълник е равен на 91 градуса, които са равни на останалите ъгли?
интересни факти
Някой от вас знаят какво триъгълник на Паскал? Задача за изграждане на триъгълник на Паскал често ще трябва да провери елементарни умения за програмиране. Като цяло, триъгълник на Паскал се отнасят до комбинаторика и теория на вероятностите. Така че какъв вид на триъгълник?
Паскал триъгълник - един безкраен аритметика триъгълник или маса с формата на триъгълник, който се формира, като се използват коефициентите двучленни. С прости думи, на върха триъгълник и стените са един и той се пълни с сума на две числа, които са разположени по-горе. Сгънете този триъгълник е безкраен, но ако очертанията му, а след това ние се равнобедрен триъгълник със симетрични редове по отношение на вертикалната си ос.
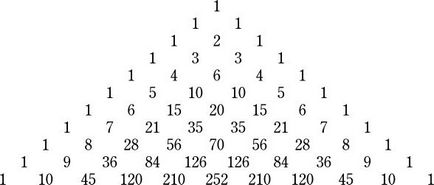
Равнобедрен триъгълник спасени от древни времена гърците и египтяните при определяне на разстоянията и височините. Например, древните гърци са определени с помощта на разстояние от разстоянието, на кораб в открито море. И древните египтяни измерват височината на пирамидите, защото на тяхната дължина от сенките, тъй като е равнобедрен триъгълник.
От древни времена, хората вече са оценени на красотата и практичността на тази цифра, тъй като формата на триъгълници ни заобикалят навсякъде. Придвижване по различни села, можем да видим покривите на къщи и други сгради, които ни напомнят за равностранен триъгълник, ще магазина, ние открихме нашите торби с храна и сокове триъгълна форма и дори някои човешки лица са с триъгълна форма. Тази цифра е толкова популярна, че тя може да се намери на всяка крачка.