височина на триъгълник, ортоцентър
Разстоянието между най-високата точка на триъгълника и на противоположната страна се нарича височина. Формално, това е най-кратък интервал между върха на триъгълника и (с възможност за удължаване) на противоположната страна.
Всеки триъгълник е с височина от 3, които се пресичат в една точка - ортоцентър. Ако използваме стандартната нотация, в триъгълника ABC. Има три височини: Аха. BHB. СНС. Тези три сегмента се пресичат в една точка - (точка Н на фигурата) на Ортоцентър на триъгълника. За тъп триъгълник (като един ъгъл по-голям от 90 °), ортоцентър е извън триъгълника.
Височината на малък триъгълник
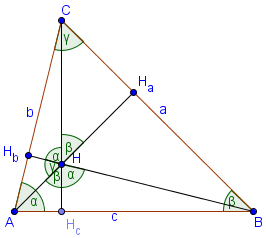
Ортоцентър - точка вътре в триъгълника.
∠ AHB = 180 - γ = α + β
∠ БХК = 180 - α = β + γ
∠ AHC = 180 - β = α + γ
∠ AHHc = β, ∠ BHHc = α, ∠ BHHa = γ
Ръст тъп триъгълник
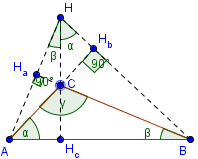
Ортоцентър е извън treugolnka.
Две височини и винаги са извън триъгълника.
∠ AHHc = ∠ CBA = β
∠ Hc HB = ∠ CAB = α
правоъгълен триъгълник
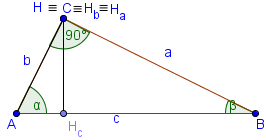
Аха височина съвпада с AC.
Това съвпада с височината на BHB преди новата ера.
Ортоцентър Н съвпада с C.
∠ ACHc = β, ∠ BCHc = α
R - радиусът на окръжност
R - радиус на вписаната
р - poluperimert: (A + B + C) / 2