Задачи, възлиза на 3 точки, платформа съдържание
Задачи, които се оценяват на 3 точки
1. Саша привлича плакат ЕАП дума кенгуру на. Идентични писма той рисува един цвят и различни букви - в различни цветове. Колко различни цветове, че ще е необходимо?
възможности:
(А), 6 (В), 7 (В), 8 (г) 9 (D) 10
2. Една услуга бързат за 25 минути и показва 7 часа и 50 минути. По кое време показва друга будилник, който изостава с 15 минути?
възможности:
(А) 10 7:00 минути (В) 07:00 25 минути (В) на 7 часа и 35 минути (D) 40 7:00 минути (D) 8:00
3. Само един от петте снимки на района на защрихованата област не е равно на бялата част. На какво?
4. Три балони струват 12 рубли повече от една топка. една топка Колко?
възможности:
(А) 4rub. (B) 6 рубли. (B) 8 рубли. (Н) 10 RBL. (Н) 12 RBL.
5. Кои от чертежите на клетките А2, В1 и NW боядисани?
6. Училището за животни научите коте 3, 4 патета, 2 Гослинг и няколко кученца. Когато учителят преброи краката на всичките си ученици се обърнаха 44. Колко кученца в училище?
възможности:
(А), 6 (В) 5 (В), 4 (г) 3 (R) 2
7. Какво не е равно на седем?
възможности:
(А) на броя на дните в седмицата, (б) половин дузина (D), броят на цветовете на дъгата
(B) броя на буквите в думата Кенгуру (D) брой на тази задача
8. Плочките на два вида са публикувани на стената, разпределен във времето. Няколко плочки паднаха от стената (виж. Фигура). Колко райета плочки падна?
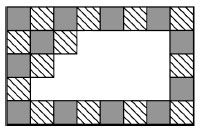
(А), 9 (В), 8 (В), 7 (г) 6 (R) 5
Задачите, които се измерват в 4 точки
11. Боб хартия поставен един след още 5 еднакви квадрати. Видимите части на площади в диаграмата са обозначени. В какъв ред Вася поставили площади?
възможности:
(А) А, В, С, D, Е (В), В, D, В, А, А (B) A, D, В, D, G (T) G, D, В, А (D ) G, B, C, D, А
12. Flea скокове на дългите стълбите. Тя може да скочи или стъпки до 3 или 4 стъпки надолу. Какъв е минималният брой на хмел тя може да се премести от земята до 22-ия етап?
възможности:
(А), 7 (В), 9 (В) 10 (Т) 12 (D) 15
13. Федя обкова правилното верига от седем домино (брой точки в съседни квадрати на два различни домино винаги еднакви). Във всички домино заедно, че е 33 точки. После се Федя получен от две домино верига (вж. Фигура). Колко точки е в полето, в което има въпросителен знак?
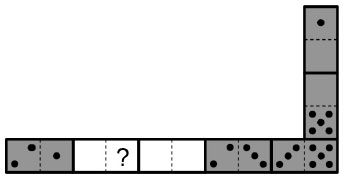
възможности:
(A) 2 (B) 3 (С) 4 (D) 5 (D) 6
14. През годината преди раждането на Кейти родителите му се заедно в продължение на 40 години. Колко години, сега Кейт, ако след 2 години, тя и родителите й заедно ще бъдат на 90 години?
възможности:
(А) 15 (В), 14 (С), 13 (D) 8 (А) 7
15. Chetveroklassnitsa Маша и брат й грейдер Миша решен проблемът с "кенгуру" конкурс за степени 3-4. В резултат на това се оказа, че Майкъл не беше 0 точки и Маша - не 100 точки. На максималния брой точки, Маша може да изпревари Миша?
Опции: (A) 92 (В) 94 (В) 95 (Т) 96 (D) 97
16. "право" обърната стрели ще странни часа (час, минута и секунда). В 12:55:30 стрелката намира, както е показано на фигурата. Това ще покаже часовника в 20 часа 12 минути?
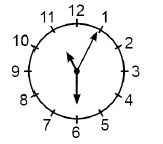
възможности:
17. Отидете риболов край петимата мъже, от една и съща фамилия: дядото, синът му, 2 и 2 внуци. Техните имена са: Борис, Грегъри V., Андрю Д., Виктор Иванов, Дмитрий Григориевич. Като дете на името на дядо ми е бил?
възможности:
(А) Andrew (В) Boris (В) Victor (D) Gregory (D) Дима
18. паралелепипеда е разделена на четири части. Всяка част се състои от 4 блока от същия цвят (вж. Фигура). В каква форма е бялата част?
19. Футболният отбор получава 3 точки за победа, равен - 1 точка, а за поражението - 0 точки. Екипът е играл 38 мача и спечели 80 точки. Какво е най-голям брой пъти, този отбор може да загуби?
възможности:
(А) 12 (В) 11 (В) 10 (Т) 9 (D) 8
Задачи, които се оценяват на 5 точки
21. Не е далеч от Венеция три острова, разположен: Мурано, Бурано и Торчело. Посетете Торчело може да бъде посетен само от начина, по който и Мурано, Бурано и още. Всяка от 15-туристите да посетят най-малко един остров. В 5 души посетиха Торчело, 13 души са посетили Мурано и 9 души - на Бурано. Колко туристи посетили острова само две?
възможности:
(A) 2 (B) 3 (С) 4 (D) 5 (D) 9
22. куб книга нарязани и внедрен. Коя от фигурите 1-5 може да се случи?
възможности:
(А) All (В), само 1, 2, 4 (В), само 1, 2, 4, 5
(Т) само 1, 4, 5 (Е) -1,2,3 само
23. Никита избра две трицифрени числа, които имат една и съща сума от числа. От повече той отне по-малко. Какво е най-голям брой може да получи Никита?
възможности:
(А), 792 (В), 801 (С) 810 (D) 890 (D) 900
24. В следобедните часове на столицата до град спринтьорка дойде и търговец. В същото време по същия път, за да се срещне тях дойде от отряд пазачи. Час по-късно охраната поздравиха бегач, дори и след 2 часа те се срещнаха на търговец, а след 03:00 пазачите са пристигнали в столицата. Колко пъти по-бързо търговец е бегач?
възможности:
(A) 2 (B) 3 (С) 4 (D) 5 (D) 6
25. Колко квадратчета образувани от специални линии, е показано на фигурата?

възможности:
(А) 43 (В) 58 (В) 62 (Т) 63 (D) 66
26. Равенството КЕН = PG * EN различни букви представляват различни ненулеви цифри и букви - същите номера!
Намери Е, ако е известно, че броят на "Кен" - възможно най-малкото.
възможности:
(A) 2 (В) 5 (B) 6 (D) 8 (Е) 9