Antiderivative и Неопределен интеграл

§ 37. примитивното и Неопределен интеграл

В предишните глави ние на специфичните функции, като се ръководят от различни формули и правила, намери своето производно. Видяхме, че производното има множество приложения: производно - скорост на движение (или, по-общо, скоростта на поява на всеки процес); производно - е наклонът на допирателната към графиката на функцията; използване на функцията производно може да се изследва и монотонността на екстремум; производно помага за решаване на проблемите на оптимизация.

Но в реалния живот, е необходимо да се реши проблемите с обратните: например, заедно с задачата за определяне на скоростта на добре известния закон на движение са се сблъскали и на проблема с възстановяването на правото на движение на известен процент. Помислете за един от тези проблеми.

Пример 1. На предната точка на подвижна материал, скоростта на неговото движение във времето Т е дадено от ф = TG. Намерете закона на движение.

Решение. Нека = S (Т) - желания закон на движение. Известно е, че е "(т) = ф" (т). Следователно, за да се реши проблема, което трябва да изберете функция S = S (т), производна от които е равна на TG. Не е трудно да се отгатне, че

Веднага ще отбележим, че примерите на решения коригират, но непълна. Ние открихме, че в действителност, проблемът има безкрайно много решения: всяка функция на формата произволна константа може да бъде законът на движение като

Тази задача е станало по-сигурно, че трябваше да се определи първоначалната ситуация: да се уточни координатата на движещата се точка във всеки даден момент, например, в т = 0. Ако, например, S (0) = s0. след това от равенството ние получаваме S (0) = 0 + C, t.e.S0 = С. Сега закона на движение се определя еднозначно:
В математиката взаимно обратни сделки са възложени различни имена, излезе със специална нотация: например, квадратура (х 2) и корен квадратен, синус (Sinh) и дъга задължително (arcsin х) и т.н. Процесът на намиране на производно на предварително определена функция се нарича диференциация и обратната операция, т.е. процес на намиране на функция за даден производно - интеграция.
Терминът "производно" може да бъде оправдано "в земно": функция Y - е (х) "ражда" нова функция в '= F' (х) • Функцията Y = F (х) действа като като "майка ", но математиката, разбира се, не я наричат" майка "или" производител ", казват те и да е, по отношение на функция у '= F' (х), първичното изображение, или, накратко, примитивен.

1. Определяне на функция у = F (х) се нарича примитивна за функция у = F (х) на предварително определен интервал X, ако за всички х от равенство X F на '(х) = F (х).

На практика междина X обикновено не се посочва, но е предназначен (като естествения домен на функцията).

1) у функция = х 2 е примитивен за функция Y = 2x, тъй като за всички х имаме (х 2) = 2x.
2) функция у - х 3 е примитивна функция у Sx 2. тъй като за всички х имаме (х 3) = Sx 2.
3) у SINH функцията е примитивен за функция у = sosh защото за всички х имаме (Sinh) = sosh.
4) Функция yavlyaetya примитивен за функцията в интервала тъй като за всички х> 0 равенството
Обикновено, знаейки производни с формула за намиране, ние лесно да се създаде таблица на формули за намиране на примитиви.

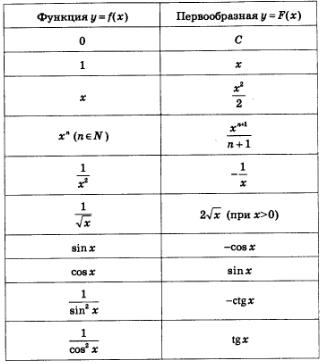
Надяваме се, че ще се разбере как тази таблица е направен: производната на който е записан във втората колона е равна на тази функция, която се записва в съответния ред на първата колона (проверете, не се мързеливи, това е много полезно). Например, за функция у = х 5 примитивен инсталиране, е функция (вж. Четвъртият ред на таблицата).

Забележки: 1. Тук се окажат една теорема, че ако = F (х) - примитивна за функция у = F (х), а след това на функция у = F (х) е безкраен брой примитиви и всички те имат формата = F (х) + С. Следователно, би било по-добре във втората колона на таблицата през добави терминът с, където с - произволно реално число.
2. За краткост понякога вместо фразата "функция у = F (х) е примитивен за функция у = е (х)», казват F (х) - примитивен за е (х) ».

2. Правилата за намиране на примитиви

Когато търсят примитиви като при намиране на производни са не само от Формула (те са показани в таблицата на стр. 196), но някои правила. Те са пряко свързани с правилата на съответните изчислителни деривати.

Ние знаем, че производната на сума, равна на сумата на производни. Това правило води до съответното правило за намиране на примитиви.

Правило 1. примитивното от сумата, равна на сумата от примитиви.

Пример 2. Намери antiderivative на функция у = 2 х + х COS.

Решение. За примитивен 2 х "; е примитивна за салатка х грях х. Така примитивен за функция у = 2 х + х COS ще служат функция у = х 2 + грях х (и, като цяло, всяка функция на формата у = х + 1 Sinh + C).
Ние знаем, че можем да вземем постоянен фактор за знака на производната. Това правило води до съответното правило за намиране на примитиви.

Правило 2: A постоянен фактор може да бъде взето извън примитивното.

Пример 3. Намерете примитиви за дадена функция:

. Fe т н а д) примитивна за грях х х е -soz; Това означава, за функция у = 5 грях х е примитивна функция у = х -5soz.

б) antiderivatives е защото х грях х; средства за примитивна функция е функция на
в) примитивна за х 3 се използва за примитивни е примитивен за х на у = 1 е функция у = х. Използването на първия и втория правила за намиране на примитиви, ние откриваме, че примитивната за функция у = 12х + 8х 3-1 е функция
Забележка. Както е добре известно, производно продукт не е равна на произведението на производното (продукт диференциация обикновено по-трудно) и производно на частния не е равно на отношението на производните. Ето защо, няма правило за намиране на продукта на един примитивен или примитивен на частното на две функции. Бъдете внимателни!
Ние се получи друго правило за намиране на примитиви. Знаем, че производното на функция у = F (KX + M) се изчислява по формулата

Това правило води до съответното правило за намиране на примитиви.
Правило 3. Ако = F (х) - примитивен за функция у = е (х), примитивното за функция у = F (KX + т) е функция

Това означава, че примитивна функция у = F (KX + т).
Смисълът на третото правило е, както следва. Ако ли, че примитивна функция у = F (х) е функция на у = F (х), a.vam трябва да се намери примитивна функция у = е (К, М +), след това се процедира, както следва: поеме същата функция като F, но вместо експресия аргумент х заместител KX + m; Също така, не забравяйте да подпише запис функция "корегиращ фактор"
Пример 4. Намерете най-примитиви за дадена функция:

Решение. а) примитивен за грях х х е -soz; Това означава, за функция у = sin2h примитивна функция ще
б) antiderivatives е защото х грях х; средства за примитивна функция е функция на

в) примитивна за х 7 служи като средство за функция у = (4-5 часа) 7 е примитивна функция

3. неопределен интеграл

Вече се отбележи, че проблемът за намиране на примитивна за определената функция в = е (х) има един разтвор. Ще обсъдим този въпрос по-подробно.

Доказателство. 1. Да Y = F (х) - примитивна за функция у = F (х) над X. интервала Това означава, че за всички X в X, X на равенство "(х) = F (х) Нека да производното на всяка функция на формата. Y = F (х) + C:
(F (х) + C) = F '(х) + С = е (х) 0 = F (х).

По този начин, (F (х) + C) = F (х). Това означава, че = F (х) + С е примитивен за функция у = F (х).
По този начин, ние сме доказали, че ако функция у = F (х) е примитивен от = F (х), след това функцията 2. Сега се докаже, че определени характеристики изгледи изчерпват набор от примитиви.

Нека = F1 (х) и у = F (х) - две примитиви за функция Y = е (х) над X. интервала Това означава, че за всички X в X интервал отговаря на връзката: F ^ (х) = F ( х); F '(х) = F (х).

Rasmotrim функция у = F1 (х) -.F (х) и намери производно: (F, (х) -F (х)) '= F [(х) -F (х) = е (х) - е (х) = 0.
Известно е, че ако производното на междина X е идентично равно на нула, тогава функцията е постоянна в Х интервал (вж. Теорема 3 от § 35). Следователно, F1 (х) -F (х) = C, например Qx) = F (х) + С

Пример 5 дадено право на промени скоростта от време V = -5sin2t. Намери движение S = S (т), ако е известно, че по време Т = 0 точка на координатната е равен на броя на 1.5 (т.е., S (т) = 1,5).

Решение. Тъй като процент - координатите, получени като функция от времето, ние първо трябва да се намери примитивно от скоростта, т.е. примитивен за функция V = -5sin2t. Една такава функция е примитиви. набор от примитиви е както следва:

За определена стойност на константата С, ние използваме първоначалните условия, съгласно който, S (0) = 1.5. Заместването с формула (1), стойности Т = 0, S = 1,5, ние получаваме:

Заместването на стойността на C във формулата (1), ние откриваме, ние се интересуваме от закона за движение:

ОПРЕДЕЛЕНИЕ 2. Ако функция у = F (х) е в интервала X примитивен в = F (х), комплектът на примитиви, т.е. множество функции на формата у = F (х) + C, наречен неопределен интеграл на функция у = F (х) и означават:

(Да се ​​чете: "за неопределен интеграл от X ЕФР де X").
В следващия раздел ще разберете какво скрития смисъл на това наименование.
Въз основа на съществуващата таблица в този раздел примитиви, долива се таблица на основните неопределени интеграли:

Въз основа на горните три правила за намиране на примитиви, можем да формулираме съответните правила на интеграция.

Правило 1. интеграл от сумата на функции е равна на сумата на интегралите на тези функции:

Правило 2: A постоянен фактор може да бъде взето извън неразделна знака:

Пример 6. Намерете най-неопределени интеграли:

Решение. а) Използване на първия и втория правилата за интеграция, ние получаваме:

Сега ние използваме 3-ти и 4-ти интеграция формули:

В резултат на това, ние получаваме:

б) Използване на трета интеграция правило и Формула 8, получаваме:

в) намиране на предварително определен ред директно неразделна ние не съответния формула или съответното правило. В такива случаи понякога помогне предварително формирани изрази идентични преобразуване, съдържащи се в подинтегрален.

Ние използваме тригонометрични формула понижаване степен:

След това ние намираме последователно:

AG Mordkovich Алгебра 10 клас

Ако имате корекции или предложения на този урок, моля свържете се с нас.

Ако искате да видите и другите корекции и предложения за уроци, погледнете тук - Образователен форум.