Изследвания по математика "как да се определи центъра на кръга," съдържание платформа
Средно общообразователно училище №1 с. Александров - Гай
Изследвания в областта на математиката:
Готови Amirov Марат, зеница 6 "и"
Клас MBOU училище №1 с. Александров - Гай
Ръководител:. MBOU учител по математика от училище №1. Александров - Гай
Александров - Гай
Глава 1 "Методи за намиране на кръга" ....................................... ..4
Глава 2, "Практическата част" ......................................................... ..6
Справки и източници ...................................................... 12
Обиколка - набор от точки, на еднакво разстояние от точка, наречена център. Въпреки това, в случаите, когато ви се предоставя само едно кръгче, намирането на центъра може да бъде трудна задача. Следователно, целта на изследванията ми: да се проучат начини за определяне на центъра на кръга. Въз основа на целите бяха определени задачи:
- намерят най-лесният начин да се определи центъра на кръга;
- сравни няколко начина за определяне на центъра на кръга;
- Практически методи за определяне на центъра на кръга.
Islledovatelskoy значение на работата се състои в това, че във всекидневния живот на хората често трябва да се намери в центъра на кръга, но не всеки знае как да го направя правилно. Затова изучаването на тази тема ще ви помогне да намерите правилното решение на проблема и да определи най-добрият вариант за хора от всякаква професия.
Когато пишете изследвания е използването на електронни източници и литература. Електронни ресурси са помогнали да се намери теоретичен материал по този въпрос, и книги, посветени на математиката са използвали за избор на цели и практическата част от работата.
Глава 1. Методи за намиране на центъра на окръжността.
1.Samy прост метод за намиране на центъра на кръга - огъване на листа хартия, на която той е съставен, като на лумена в кръг беше сгънат точно на половина. Получената гънки линия ще бъде едно от предварително определен диаметър на кръга. След това листът може да се вкара в друга посока, при което се получава втори диаметър. Пресечната точка е в центъра на кръга.
2. да намерите центъра на кръга, първо трябва да го въведете в площада. Това означава, че всички страни на правоъгълника трябва да докосват кръга. За да направите това, изпълнете с линийка четири прави линии. Сега се свърже двата диагонално противоположни ъгли. Уверете се, че ъгълът на линия разби квадрат на две равни части. Свързване с права всички четири квадратен ъгъл. тези точки на пресичане е центъра на кръга.
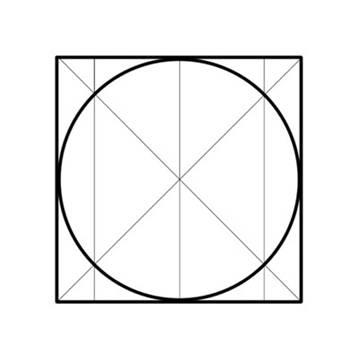
3. За всеки триъгълник на окръжност се намира в пресечната точка на медианите вертикалите. Ако този триъгълник - квадрат, в центъра на описаните окръжности винаги съвпада с средата на хипотенузата. Следователно, ако един кръг вписан в правоъгълен триъгълник, неговата хипотенуза е диаметърът на този кръг.
Като шаблон за този процес всеки подходящ прав ъгъл - в сградата на училище или квадратна или просто парче хартия. Поставете горната част на десния ъгъл на всяка точка от окръжността и маркира къде кръг пресече граничния страна на ъгъла. Тази точка край диаметър.
По същия начин се намери втори диаметър. В точката на пресичане
4.The кръгъл елемент налага лист хартия, така че един ъгъл е най периферен ръб или кръг. И това бележи мястото, където листа влиза в контакт с другите краища на кръга. Отбелязваме тези точки.

Ние извършваме по права линия между отбелязаните точки. Разстоянието между тях е диаметърът на този кръг. Ние нарязани излишната хартия и изготвят по права линия на детайла - диаметър.

Достатъчно е да се движат нашия триъгълник на друга длъжност и направи още един кръг с диаметър като веднага в диаметър пропускателен пункт и получаваме желания центъра на кръга ...
5. Диаметърът и радиусът на кръга.
Диаметърът на кръга - отсечка, свързваща двойка най-отдалечени една от друга точки на окръжността, минаваща през центъра на кръга. "Диаметър" Думата произлиза от гръцката дума "diametros" - кръст. Обикновено диаметър D на обозначава латинската буква или символ Ø.
Диаметърът може да бъде намерена чрез формулата: D = 2R, където диаметъра е равно на два пъти радиуса на кръга.
Радиус - разстояние от центъра до всяка точка на обиколката. Определени Латинска R.
Ако е известно, радиусът на кръга, например, е равна на 8 см, това означава, че D = 8 = 2 * 16 cm.
Радиусът на кръга определя по формулата. R = D: 2
Глава 2, "Практическата част"
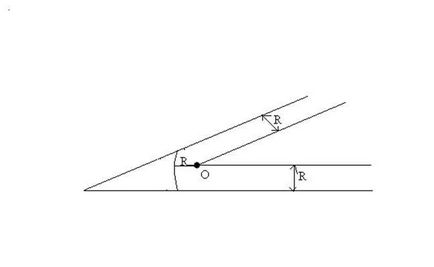
1) Директни предмети заоблени ъгъл дъга радиус R
С центрове в точки А и В са две сграда окръжност с радиус R; С - тяхната пресечна точка. Дъгата на окръжност с радиус R центриран в точка С е желаният закръгляване.
Произволни предмети заоблени ъгъл дъга радиус R
Решение: На разстояние R от страни на ъгъла управлението на съответната успоредно на тях директно. За - пресичането им. След това, се конструира окръжност с център О, радиус R
Като се има предвид две успоредни линии, както и точка А между тях. Как да се изгради един кръг допирателна на линиите за данни и минаваща през дадена точка?
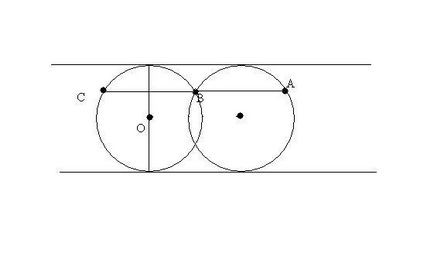
1) се конструира всеки кръг допирателна към две прави линии (центъра на кръга Определят го разделя на половина)
2) Пряка равенство през равни данни. Тя пресича застроена кръг в точки Б и В. Преди те построен в центъра на кръга на AB или AC.
Технически проблеми по изграждането на фигурата
Как да се използва водопровод маркер гон диаметър кръгла мярка недостъпни части.
Възможно ли е устройството е показано на фигурата чрез прилагане на една единствена намерите центъра на кръга?
"Как да се открие центъра на кръга?" - въпрос, на който трябваше да отговори на анкетата. По този начин, Аз открих няколко начина за изграждане на центъра на кръга: 1) tsentroiskatel - прав ъгъл. РАБОТА: вписан ъгъл въз основа на диаметъра. 2) Tsentroiskatel - ъгъл с ъглополовящата. РАБОТА: диаметър на кръга е разположен на ъглополовящата на ъгъла, описан за okruzhnosti.3) Tsentroiskatel - чифт взаимно перпендикулярни линии. Принцип на действие: от диаметъра, извършена на мястото на контакт, перпендикулярна на допирателната. 4) Tsentroiskatel - чифт взаимно перпендикулярни линии. Как работи: акорд, акорд перпендикулярна на другия и минаваща през средата на него, има диаметър.
Съответно, обект на работата ми досега: разглеждане на няколко метода за намиране на кръга центъра на всяко възможно да се избере оптималния вариант.
О, математика земята!
Бъдете горди, красиви, е,
Вие всички науки собствена майка,
И те ти се грижиш.
Вашите изчисления величествено
Да доведе до планети кораби
Не за празничната забавно
И в името на гордостта на Земята!
Справки и източници
1.Zhurnal "Математика в училище» №20 1989.