Как се изчислява ефективния лихвен процент

Всъщност, по смисъла на ефективния лихвен процент е съвсем проста - той е проектиран да отразява реалната цена на кредита до гледна точка на заемополучателя, тоест, да се вземат предвид всички нейни странични плащания, пряко свързани с кредита (различни от плащанията на самия заем). Например, такива странични плащания са известни "скрити" банкови такси - такси за откриване и поддържане на сметки за получаване парични средства в брой и т.н. Друг пример: Ако вземете кола заем, банката се задължава да застрахова сте купили колата за целия период на кредита. В този случай, застраховката ще бъде задължително за вас надясно плащания (макар и не на самата банка, а застрахователните компании) .What е интересно, централната банка, търговските банки са длъжни да разкриват на ефективния лихвен процент по кредитите и дори осигури формула за изчисляване не посочва какви конкретни плащания трябва да бъдат включени в това изчисление. В резултат на това различните банки имат различни гледни точки по въпроса на: много, например, не са включени в изчисляването на времето осигурителни вноски.

Въпреки това, най-правилно и просто изглежда като подходът, който при изчисляването на ефективния лихвен процент включва всички такси, които са необходими, за да се получи този заем. По-специално, всички задължителни осигурителни вноски.

След като приключва с този проблем, сега сме в състояние да даде на строго определение на ефективния лихвен процент.

Ефективен лихвен процент - това е сложна лихва, изчислена на предположението, че всички плащания, необходими за получаването на този заем, ходят на изкуплението си.

Това означава, че ако резултатът от размера на заема S0 заемател е принуден да се извършват плащания R0. R1. R2. RN в момент t0 моменти = 0, t1. t2. TN съответно (което включва и двете плащания на самата заема и от страна на комисията, осигурителни вноски и т.н.), ефективният лихвен процент аз разбрах от отношението

Ефективният лихвен процент се използва предимно за сравнение на различните банкови оферти и изчисляването на точната дата на плащанията на Комисията са обикновено неизвестни. Ето защо, ако плащанията се извършват чрез формално равни интервали от време продължителност # 964; (Месечни, тримесечни и т.н.), след това (1) е:

Ако кредитополучателят всички плащания, с изключение може би на първия, същата (R1 = R2 = = Rn = R.), След това в съответствие с формула изчисляване на сумата на крайно геометрична връзка за определяне на ефективната лихва ще бъде:

За съжаление, намирането на точната стойност на ефективния лихвен процент, дори и в този сравнително прост случай е невъзможно, така че трябва да го изберете (най-добрия начин - с помощта на специален числен метод). Как точно - това ще бъде обсъдено по-нататък.

За заема със следните условия:

срока на кредита - 3 години;
лихвен процент (ние ще го означаваме с к) - 18% годишно;
погасяване схема - месечна равна (фиксирана) с такси;
за таксата за подреждане на кредита - 1% от сумата;
месечна такса за поддържане на сметката на кредита - 0.1% от размера на кредита

Ефективният лихвен процент ще бъде 22,8%. За да се тества намерят стойностите на всички променливи присъстват във формула (3):

R0 = 0,01 х S0;
п = 36;
# 964; =;
J = 0,18;
анюитетни вноски :;
R = A + 0,001 х S0 ≈ 0,0372 х S0;
I = 0228;
месечно ефективната лихва IM = (1 + I) # 964; ≈ 1,017262.

Замествайки тези стойности във формулата (3), след намаляване на S0 лесно да се провери валидността на половете (освен ако, разбира се, не обърна внимание на грешката от закръгляване):

Общ метод за изчисляване на СУЕ

Така че, ние се отбележи, че размерът на ефективния лихвен процент, дори и за относително прости операции по заеми не могат да бъдат намерени с помощта на формула. Тук идват на помощ на така наречените числени методи. което даде възможност за краен брой стъпки, за да се изчисли приблизителната стойност на неизвестно количество с необходимата точност.

Общ метод за приблизителното изчисление на ефективния лихвен процент, които ще бъдат обсъдени по-нататък, може да се прилага за всички заеми, плащания, за които се извършват на редовни интервали. Нейната основа е числен метод на Нютон. същността на което, в общи линии, е както следва.

Да предположим, че е необходимо да се намери решение на F в уравнение (х) = 0, където е (х) - диференцируема функция. След това, при определени условия, последователност от числа х (к)>, която е първа стойност х (0) е избран независимо, и всяка следваща формула намира

клони към точното решение на това уравнение. В момента сме без значение какви са условията, можете да лесно да намерят, ако искате информация за ограниченията на метода на Нютон.

Нека сега да видим как да се използва този метод за изчисляване на ефективния лихвен процент.

Въвеждаме нова стойност срещу # 964; = (1 + I) - # 964. която се нарича фактор намаление за периода от време, # 964;. С помощта на формулата (2), представляваща общият коефициент за намиране на ефективен лихвен може да бъде пренаписана, както следва:

Намирането на основата на това уравнение е еквивалентно на намиране на корен на функцията

Тази функция има само един положителен корен (ни интересува само положителните корените) и тя се намира в интервала (0, 1). Това корен могат лесно да бъдат открити чрез използване на метод на Нютон, предварително изчисляване на производно на F функция (х):

Сега, избора на първоначалното приближение х (0) = 1, с формула (4), ние се получи последователност от числа х (к). приближава до точната стойност на V # 964;. Приблизителната стойност на неизвестен ефективен лихвен процент е намерена от следната зависимост:

(Ако приемем, че ние сме готови изчисляване на стъпка номер N).

Ефективният лихвен процент за размера на кредита S0 = £ 1,000 Великобритания, издаден през годината под проста лихва, к = 20%. Кредитополучател за погасяване на кредита бяха направени следните частични плащания:

R1 = 600 паунда след 3 месеца (t1 = ¼) след началото на операцията;
R2 = 310 паунда след 9 месеца (Т2 = ¾) след началото на операцията;
R3 = 194,25 паунда годишно (t3 = 1) след началото на операцията.

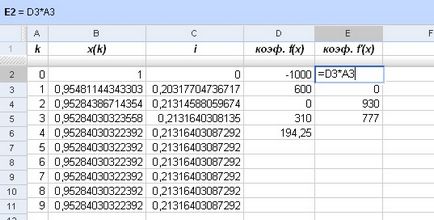
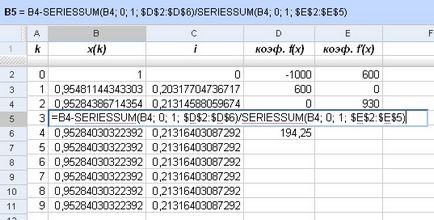
Тъй като периодът от време, # 964; изберете един блок (# 964 = ¼). В съответствие с метода, описан по-горе, ще се въведе допълнителна функция

и да намерят неговите производни:

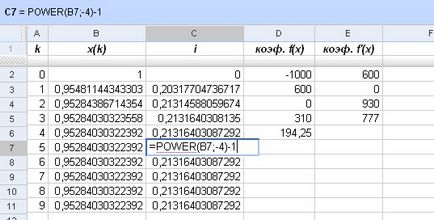
Сега, избора на първоначалното приближение х (0) = 1, с формула (4) конструиране на последователност на приблизителните стойности на намаление фактор V # 964; и ефективния лихвен процент и:

аз ≈ 0,21316403087292

Още на петия етап на изчисление доведе до същия резултат като през предходната година, и с точност, че вие сте едва ли някога ще бъде в състояние да се наложи. Този резултат е повече от 1,3% по-висока от обявената (номинален) лихвен процент по кредита, въпреки че не е имало скрити такси или всякакви други допълнителни плащания.

Как се изчислява ефективния лихвен процент

Обърнете внимание на следните точки:

Сега нека разгледаме по-сложна, но по-скорошен пример.

Заем от 24 хиляди евро, издадени от две години при 12% годишно, платим на месечни вноски в съответствие с диференцирана схема. Аранжиране такси в размер на 1% от сумата. В допълнение, всеки месец на кредитополучателя ще се начислява такса за поддържане на сметката за заем в размер на 0.1% от размера на кредита. Трябва да намерим ефективен лихвен процент на кредита.

На първо място, ние конструираме графика за погасяване на кредита (с изключение на структурата на таксите). Плащанията към погасяване на кредита образуват аритметична прогресия с първоначален срок

А1 = (+ 0,12 х) х 24 000 = 1240 евро

- (0,12 х х 24,000) х = - 10 евро.

В допълнение, при получаване на кредита кредитополучателят трябваше да плати 0,01 × 24 000 = 240 евро, а всеки месец с него доплащане измерване 0,001 × 24 000 = 24 евро. Следователно, за графика на плащанията по заема е, както следва:

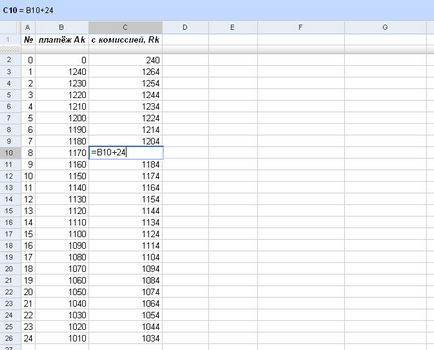
Фиг. Графикът на плащанията по заема

Стойностите на колона "с комисията, Rk», с изключение на първия (индекс 0), съвпадат с коефициентите на правомощията на х в функция е (х), които ще се използват при изчисленията. За първи коефициент (степен нула х) е необходимо от първоначално плащане R0 = 240 изваждащ размер на кредита (формула горе вляво):

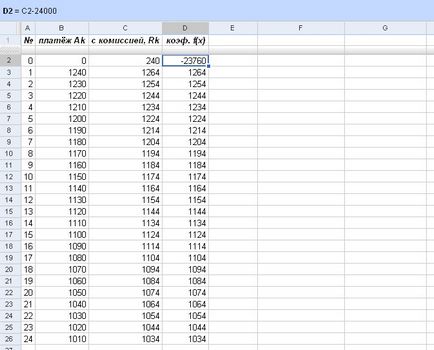
Фиг. Намирането на коефициентите на функцията F (х)

Коефициентите на сили на х производно F "(X) са вече известни принципа:

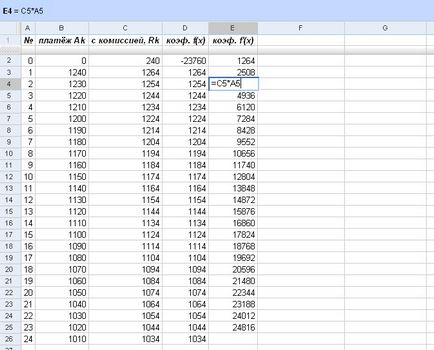
Фиг. Намирането на коефициентите на производно F '(х)

Сега, най-накрая, можете да използвате метода на Нютон за намиране на месечна дисконтов фактор (формулата в горния ляв ъгъл):

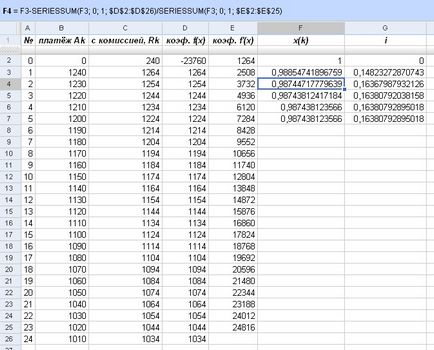
Фиг. Намирането на месечна дисконтов фактор

Едновременно с изчисляването на месечната фактор отстъпка се самоопредели ефективен лихвен процент аз:

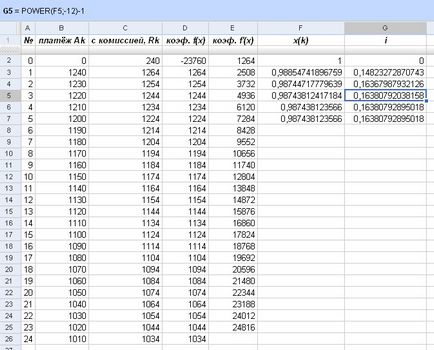
Фиг. Намирането на ефективния лихвен процент

Както в примера в предходния параграф, метод на Нютон ни доведе до окончателен отговор само на пет изчисления: на ефективния лихвен процент по кредита се разглежда, е приблизително равно на 16,38%, 4,38% по-висока от номиналната ставка.

Изчисляването на EPS за анюитет

Методът, че ние разгледахме по-горе, когато се използва правилно, е доста удобно. Но в някои случаи, а именно за погасяване на анюитет схема на кредита, ефективният лихвен процент може да се намери дори и бързо и лесно. Всъщност, основното предимство на метода, който ще бъде дискутирано по-нататък, е по-компактен.

Препишете (3) - съотношението за определяне на ефективния лихвен процент, който е валиден за погасяването на заем анюитетни - използване на вече познатите ни дисконтов фактор срещу # 964; = (1 + I) - # 964; :

След това, като се използва формула (4) може да бъде последователност от числа х (к)>, приближава до точната стойност отстъпка фактор V # 964; ,

Ефективният лихвен процент по заема от първия пример. Условия припомнят, са както следва:

срока на кредита - 3 години;
й интерес процент - 18% годишно;
погасяване схема - месечна равна (фиксирана) с такси;
за таксата за подреждане на кредита - 1% от сумата;
месечна такса за поддържане на сметката на кредита - 0.1% от размера на кредита.

В допълнение, за да бъдат конкретни, ние приемаме, че размерът на заема е 12 млн. Рубли.

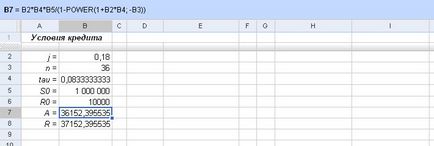
Фиг. Като прибавим към началните условия

Следващата стъпка - е изчисляване на коефициентите на F функция (х):

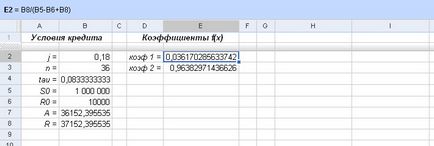
Фиг. Изчисляване на коефициентите на е (х)

Първият коефициент в комбинация е първоначално сближаване на х (0). Преместете го в съответната клетка и метод на Нютон изчислява броя на месеците на фактора приближените отстъпка (забележите формулата в горния ляв ъгъл):

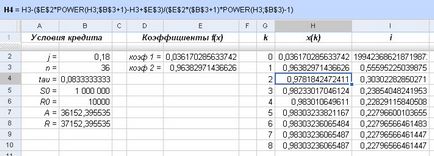
Фиг. При изчисляването на месечната отстъпка фактор

В същото време ние се изчисли приблизителната стойност на ефективния лихвен процент I:

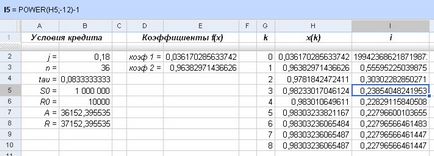
Фиг. Изчисляването на ефективния лихвен процент

Както можете да видите, след осем изчисления, ние за пореден път потвърди, че на ефективния лихвен процент по кредита се разглежда, е около 22,8%, с 4,8% повече от номинала.

Забележка. След попълване на мухъл, подобна на тази, показана на фигурите, след това ще бъде в състояние веднага да се определи ефективния лихвен процент на всеки заем се погасява в съответствие със схемата за рента, само промяна на първоначалните условия.

В заключение, искам да направя още една важна обща забележка. Считаме, методът е гарантирано да се сближат (т.е. да доведе до желаната стойност на дисконтовия фактор и ефективния лихвен процент), ако първоначалната стойност на избраната стойност (7). Ако вземем друг първоначалното приближение, методът може да се приближават към втория основата на F функция (х) - единица (съответстващи на стойността на ефективно интерес процент е нула). Така например, в примера, който се обмисля, това се е случило, за да, ние приемаме като първоначална приближение, всяко число по-голямо от 0,992.

И още един общо наблюдение върху избора на числен метод. Има голямо разнообразие от числени методи, много от които също биха могли да се прилагат за решаване на нашите проблеми. метод на Нютон е избран, защото това е, по мое мнение, на баланс между използването на скоростта на сложност и конвергенция (помните, ние сме в един от примерите, не е извършило повече от осем изчислителни). Там са по-бързи, но са по-трудно да се разбере методи. Има по-прости методи, с по-малко ограничения и гарантирано конвергенция, но изисква голямо количество изчисления. Например, ако бяхме използвали в последния пример, добре познат метод на проста итерация. с цел постигане на необходимата точност, ние ще трябва да се направи сто изчисления. Ясно е, че тези изчисления прави програмата си.

Предишен ◈ Следващото

Как се изчислява ефективния лихвен процент