Класификация на точки на прекъсване - studopediya

Разглеждане функция е (х), непрекъснато в близост до точка x0 на, с изключение може би това се точка. От определянето на точката на прекъснати функции, следва, че х = x0 е точка на прекъсване, когато функцията не е дефинирана в този момент, дали или не е непрекъснат.

Трябва също да се отбележи, че непрекъснатостта на функцията може да бъде едностранно. Нека обясним това по следния начин.

Ако едностранно ограничение. тогава функцията се нарича непрекъсната отдясно.

Ако едностранно ограничение. тогава функцията се нарича непрекъсната в ляво.

x0 точка нарича точка на прекъсване на е (х), ако е (х) не е определено по x0 или не непрекъснато в този момент.

x0 точка се нарича точка на прекъсване от първи вид 1. Ако в този момент е (х) функция е ограничен, но не е равна на една от друга на лява и дясна граници.

За да не се изисква условията на това определение, че функцията е дефинирана в точката х = x0 е достатъчно, че тя се определя от ляво и дясно от него.

x0 точка се нарича точка на прекъсване 2 - втория вид. Ако в този момент F функция (х) има най-малко един от едностранни граници, или най-малко един от тях е безкраен.

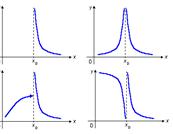
Ако стойностите на краищата на пропастта са едни и същи, а след това има разминаване, което трябва да или същите стойности се различават от стойностите на функцията в точката. или функция в този момент не е определена. Ако в този случай замяна (или да удължи определение) функцията в точката. получената функция ще е промененият непрекъсната в точката, и разликата в точката ще изчезне; откъдето идва и името на тази празнина - за еднократна употреба.

подвижен прекъсване точка - когато съществуват лявата и дясната граници и са равни. но не съвпада със стойността на функцията в точка x0 или функцията не е дефинирана в x0.