Скорост и ускорение точка
Скорост и ускорение
точка на скоростта
В предишна статия движение на тялото или точка дефинира като промяна на позицията в пространството с течение на времето. С цел по-пълно да се опише качествените и количествените аспекти на движение въвежда концепции за скорост и ускорение.
Скорост - движение мярка кинематична на една точка, която характеризира степента на промяна на позицията си в пространството.
Скоростта е количество вектор, Т. Е. Тя се характеризира не само модул (скаларна компонент), но също така и по посока в пространството.

Както е известно от физиката, еднакво скоростта на движение може да бъде определена дължина на пътя премества за единица време: V = S / T = конст (приема се, че произхода и начина, по едно и също време).
В прав скоростта на движение и постоянно модул и посока, и то съвпада с траекторията на вектор.
скорост звено в системата SI се определя от дължината / час т. Е. м / сек.
Очевидно е, че в момента на криволинейни скорост на движение ще се колебае в посока.
За да се определи посоката на вектора на скоростта във всяка времева точка в криволинейна движение, се разделят на траекторията в безкрайно раздели на песен, която може да се счита (като резултат от тяхната незначителност) праволинейни. Тогава при всеки сайт условно скорост ил такива праволинейно движение е насочено по хордата и хордата, от своя страна, намалява в безкрайна дължина дъга (Δs клони към нула), ще съвпадне с тангентата към дъгата.
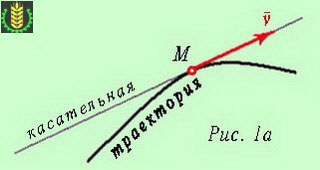
От това следва, че когато криволинейна вектор скорост на движение при всяка точка от време съвпада с допирателната към траекторията (фиг. 1а). Праволинейно движение могат да бъдат представени като частен случай на извитата движение по дъга, чийто радиус подходи безкрайност (траектория съвпада с допирателната).
В неравномерно движение на точка модул на скоростта варира с времето.
Представете точка, чието движение се определя по естествен начин чрез уравнението S = F (т).
Ако в рамките на кратък период от време ATi, точка е отишло Δs. Тогава средната му скорост е равна на:
Средната скорост не представлява истинската скорост във всеки един момент от време (вярно скорост се нарича още миг). Очевидно е, че по-малкият интервал от време, за който се определя средната скорост, колкото по-близо е до стойността на моментната скорост.
Вярно (моментално) процент е границата, до която средната скорост тенденция по време на ATi,, клони към нула:
V = Лим т → Вав при 0 или V = Лим (Δs / АТ) = DS / DT.
По този начин, числова стойност, равна на истинската скорост V = DS / DT.
Истинският (моментално) скоростта на движение във всяка точка е първата производна на координатите (т. Е. разстоянието от произхода на движение) с течение на времето.
Когато АТ отива към нула, Ds и клони към нула, и, както вече видяхме, вектора на скоростта се отнася по допирателната (т. Е. същата като истински скорост вектор V). От това следва, че лимитът на условно скоростта на вектор ин. равно на съотношение граница на вектор за движение точките на безкрайно интервал от време е равно на истинските скорост векторни точки.
Ускорение точка в праволинейно движение
Като цяло, движение на точките с време-различна скорост, наречена ускори, като се има предвид ускорението причинява намаляване на скоростта, отрицателна. Понякога движението, при който скоростта намалява с времето, наречена забави.
Ускорение има кинетичен мярка за степента на промяна на точката във времето. С други думи - ускорението - е скоростта на промяна на скоростта.
Както скорост, ускорение е количество вектор, Т. Е. Не характеризира само с модул, но също така и по посока в пространството.
В праволинейни вектор скорост на движение винаги съвпада с траекторията и така скоростта на вектор промяна също съвпада с траекторията.
Разбира се по физика е известно, че ускорението е промяната в скоростта за единица време. Ако в рамките на кратък период от време ATi, скорост точка се е променило в Av. средната ускорение над определен период от време е: ACP = Δv / АТ.
Средно ускорение не дава представа за истинската стойност на степента на промяна в даден момент. Очевидно е, че по-малките разглеждания интервал от време, през който се наблюдава промяна на скоростта, по-близо до стойността на ускорението е истинската (моментално).
От тази дефиниция: вярно (моментно) ускорение е границата към който средният ускорение по време АТ. клони към нула:
и когато Аср = Лим т → 0 или Lim Δv / АТ = DV / DT.
Като се има предвид, че V = DS / DT. Ние получи: а = DV / DT = г 2 S / DT 2.
Истинската ускорение в праволинейно движение е равен на първата производна или втората производна на координатите на скоростта (разстоянието от произхода на движение) с течение на времето.
Единицата за ускорение - метър разделен на секунда на квадрат (m / и 2).
Ускорение точки в криволинейни движение
Когато се движат по извита пътека посока промени точка на скоростта, т.е.. Вектор F скорост е променлива.
Представете си една точка М, която с течение на времето АТ. движат по извита пътека, той се премества в положение на М1 (фиг. 1).
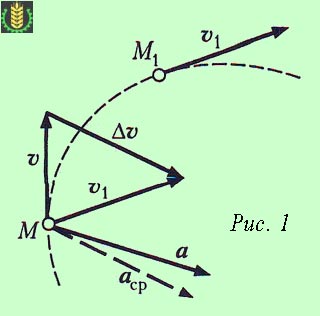
вектор нарастване (промени) означен скорост Δv. тогава: Δv = v1 - об.
За вектора Δv прехвърли вектор v1 в точка М и изграждане на триъгълника на скорост. Ние дефинираме вектора на средно ускорение:
Аср вектор успоредна на вектора Δv. като количеството вектор чрез разделяне скаларна посока вектор не се променя.
Векторът на истинската ускорение е ограничение, към който съотношението на скоростта на нарастване тенденция вектор на съответния интервал от време, когато последният клони към нула:
а = Лим Δv / АТ в т → 0.
Такова ограничение нарича вектор производно.
По този начин, вярно ускоряване на точката в криволинейна вектор за движение е равно на времето производно на скорост.
Фигура 1 показва, че вектор ускорение в криволинейна движение винаги е насочено към вдлъбнатината на пътя.
От вектора получава пряко изчисли ние не може след ускоряването на криволинейна движение ще определи косвени методи. Например, ако движението на една точка, разположена в естествен начин, а след това се прилага теоремата на прогнозите за ускорение тангента и нормално. За да се разбере същността на тази теорема, е необходимо да се разгледа концепцията за линии на кривина на кривите.
Концепцията на кривината на криви
Разглеждане на извитата траекторията на точка М (фиг. 2а).
Ъгъл Δφ между допирателни към кривата на две съседни точки се нарича ъгълът на съседство.
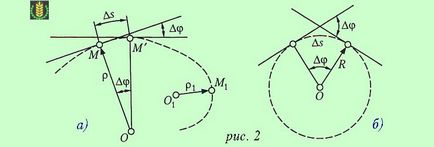
Кривината на кривата в този момент е съотношението непосредствена близост на ъгъл граница Δφ, съответстваща на дължината на дъгата Δs, когато последният клони към нула.
Означаваме кривината на писмо к. след това:
К = Лим Δφ / Δs когато Δs → 0.
Да разгледаме окръжност с радиус R (вж. Фигура 2В).
Тъй Δs = RΔφ. след това:
К = Лим Δφ / Δs = Лим Δφ / RΔs = 1 / R (когато Δs → 0).
Следователно, кривината на окръжност във всички точки еднакви и равни на к = 1 / R.
За всяка точка на кривата може да избере един кръг, чиято кривина, равна на кривината на кривата на този етап. р радиуса на този кръг се нарича радиусът на кривината на кривата в даден момент и центъра на този кръг, - центъра на кривина.
По този начин, кривината на кривата на този етап е реципрочен на радиуса на кривата на този етап.
Очевидно е, че кривината на права линия е нула, и тъй като радиусът на кривината на такава линия е равна на безкрайност.
Теорема на прогнози за ускоряване на допирателната и нормалата
Проекцията на ускорение на допирателната към траекторията се нарича допирателна (тангенциален) ускорение и ускоряване на проекцията на нормалата към допирателната - нормално ускорение.
Теорема: нормално ускорение равно на квадрата на скоростта разделен на радиуса на кривината на пътя в този момент; тангенциално ускорение - първата производна на скоростта по отношение на времето.
Доказателството се основава на геометрични конструкции, като се вземат предвид зависимости споменати по-горе преместване, скорост и ускорение спрямо времето. В тази книга, доказателството не е дадено; ако е необходимо, е възможно да се помисли за други източници на информация.
Така че, на базата на теоремата на ускорение, можем да запишем:
ап = о 2 / ρ; aτ = DV / DT.
Анализ на формулата на допирателната и нормалното ускорение, можем да заключим, че тангенциално ускорение характеризира скоростта на промяна е само в абсолютна стойност и нормално - само в посока.
Знаейки, че стойността на нормалното и тангенциално ускорение, можете да се изчисли общата ускорение на точка, като се използва питагорова теорема:
посока ускорение: COS (aτ, а) = aτ / г.
Често тангенциална и нормалното ускорение не се считат за прогнози, но като компоненти на пълна ускорение, г. Д. като вектор количества.
нормален вектор ускорение винаги насочени към центъра на кривина, така че ускорението понякога се нарича центростремителна.
Видове движение точки, в зависимост от ускорението
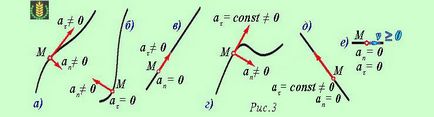
Анализ на формула тангенциална и нормално ускорение са следните видове точки за движение:
ап = о 2 / ρ ≠ 0; aτ = DV / DT ≠ 0. - неправилна криволинейна (Фигура 3а).
ап = о 2 / ρ ≠ 0; aτ = DV / DT = 0. - еднакво криволинейна (Фигура 3b.);
ап = о 2 / ρ = 0; aτ = DV / DT ≠ 0. - праволинейни неравномерно (Фигура 3b.);
aτ = DV / DT = конст ≠ 0; ап = о 2 / ρ ≠ 0. - ravnoperemennoe криволинейна (Фигура 3а.);
aτ = DV / DT = конст ≠ 0, ап = о 2 / ρ = 0. - ravnoperemennoe праволинейни (Фигура 3d.);
ап = о 2 / ρ = 0; aτ = DV / DT = 0. - еднакво линейна (движение без ускорение) (Фигура 3д.).
Теореми на проекцията на скоростта и ускорението на координатната ос
Ако движението на точките координатните определени метод, разстоянието (изместване), скорост и ускорение по време на интервала от време АТ могат да бъдат намерени проекцията на тези стойности на оста на координатната. Очевидно е, че всяко увеличение на координати, когато ATi, клони към нула също клони към нула, а границата от увеличението може да бъде определена от диференциални връзки, установени теореми за прогнози скорост и ускорение:
Теорема: скорост проекция върху оста на координатната е първото производно на съответното координира време:
Теорема: проекция на координатната ос на ускорението е втората производна на съответните координира време:
брадва = г 2 х / ATi, 2 ай = г 2 г / ATi, 2 Я = г 2 Z / ATi, 2.
Познаването на скорост или ускорение на проекцията на координатните оси, е възможно да се определи големината и посоката на вектора на някоя от тези стойности с помощта на Питагоровата теорема и тригонометрични отношения.