Точка на прекъсване и техните видове
Определяне на точки на прекъсване и техните видове е продължение на темата за непрекъснатост на функции. Visual (графичен) обяснение на точките на прекъсване се прилага също за разлика от концепцията за непрекъснатост.
Точките на данни, които не са свързани помежду си, се наричат точки на прекъсване. Графиката на такава функция, потоци прекъсване на най х = 2 - - долу.
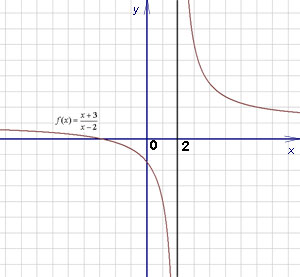
Обобщение на гореизложеното е следното определение. Ако функцията не е непрекъсната в точката, а след това има прекъсване в този момент и самата точка се нарича точка на прекъсване. Прекъсвания са от първи вид и втори вид.
С цел да се определят видовете (характер) функция точки за пробив, което трябва да намерим границите на сигурност. Затова е полезно да се отвори нов прозорец в съответния урок.
Намиране на точки на прекъсване може да бъде като независим задача, както и част от по-пълно изследване на функцията и интригите.
първият вид прекъсване точка: функцията там като краен (т.е. да не е равна безкрайност ..) в лявата граница и десния край лимит, но функцията не е дефинирана или в лявата и дясната граници са различни (не равни).
Точка на сменяем прекъсване от първи вид. Отляво и отдясно граници са равни. В този случай, е възможно да се разшири определението на функцията в точката. Разширяване на определението на функцията в точката, казвайки просто, това означава да се осигури връзка с това посочва, между които има момент, в който установи, равна на една от друга на лява и дясна граници. Във връзка с това трябва да бъде само една точка, в която трябва да се намери стойността на функцията.
Пример 1. За да се определи функцията на точка почивка и форма (характера) на точки на прекъсване.
Решение. Не е дефинирана функция в точката. Ние считаме, отляво и отдясно границите на функцията в този момент:
Отляво и отдясно са границите следователно точка - разпръснати сменяем прекъсване от първи вид.
Възможно е да се разшири определението за функция:
Графиката на точката на прекъсване с - съгласно пример.
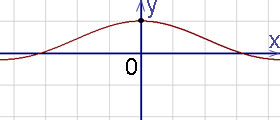
За изчисляване на границите на самоконтрол, можете да използвате онлайн границите калкулатор.
несменяем точка (край) от първия вид прекъсване. Има лява и дясна граници, но те са различни (не е равно). Невъзможно е да се разширят определението на функцията. Лимитът за разлика се нарича скок.
Пример 2. Определяне на прекъсване функция и форма (знака) на точки на прекъсване на функцията
Решение. Очевидно е, че промените в изразяването на точката на функция. Намерете най-ляво и дясно границите на функцията в този момент:
Отляво и отдясно границите не са равни, следователно точка - несменяем точка (край) от първия вид прекъсване. Графиката на точката на прекъсване с - съгласно пример.
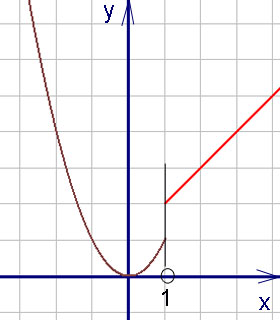
За изчисляване на границите на самоконтрол, можете да използвате онлайн границите калкулатор.
Намиране на точки на прекъсване може да бъде като независим задача, както и част от по-пълно изследване на функцията и интригите.
вторият вид прекъсване точка: точката, в която най-малко един от праговете (наляво или надясно) - безкрайност (равна на безкрайност).
Пример 3. Определяне прекъсване функция и форма (знака) на точки на прекъсване на функцията
Решение. От нивото на експресия, наблюдавани при д, че точката не е определена. Намерете най-ляво и дясно границите на функцията в този момент:
Едно от ограниченията, е безкраен, така че точката - една точка на прекъсване от втория вид. Графиката на точката на прекъсване с - съгласно пример.
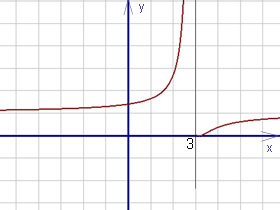
За изчисляване на границите на самоконтрол, можете да използвате онлайн границите калкулатор.
Намиране на точки на прекъсване може да бъде като независим задача, както и част от по-пълно изследване на функцията и интригите.
И няколко примера.
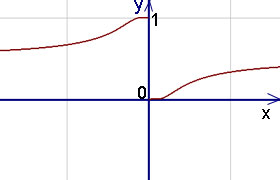
Пример 4. Определяне на прекъсване функция и форма (знака) на точки на прекъсване на функцията
Решение. От нивото на изразяване на 2, че точката не е определена. Намерете най-ляво и дясно границите на функцията в този момент:
Ограниченията не са равни и ограничени, така че точката - точката на непоправими разкъсване от първи вид. Графиката на точката на прекъсване с - съгласно пример.
За изчисляване на границите на самоконтрол, можете да използвате онлайн границите калкулатор.
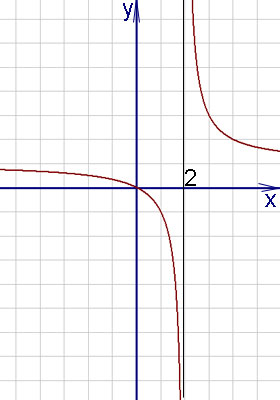
Пример 5. Определяне прекъсване функция и форма (знака) на точки на прекъсване на функцията
Решение. Ясно е, че точката не е определена. Намерете най-ляво и дясно границите на функцията в този момент:
И двете граници са безкрайни, така че точката - вторият вид на точката на прекъсване. Графиката на точката на прекъсване с - съгласно пример.
За изчисляване на границите на самоконтрол, можете да използвате онлайн границите калкулатор.